全エネルギーの計算
速度分布を導き出した元々の動機は,容器の中の粒子群の全エネルギーを計算したいが為だった.
とりあえずは単一種類の粒子群について考えよう.質量がどれも同じだから扱いが簡単だ.容器全体で合計個の粒子があるとする.速さが
の範囲にある粒子の数は,前回の結果を使って,
だと計算できる.これに個々の粒子の運動エネルギーである
を掛けてやれば,
の範囲にある粒子の運動エネルギーが求まるだろう.それを全ての速度について積分してやれば,全粒子の運動エネルギー
が計算できることになる.
この計算の途中で,
という公式を使ったが,これは例によって別のページに説明しておいた.
さて,ここまでの結果から・・・うーん,特に大した事は分からないなぁ.でもこれが少し後の方で役に立つのである.
圧力の正体
次に気体の圧力を分子運動論で説明してみよう.気体の圧力というのは,多数の粒子が容器の壁を叩きつけることで生じているのだと考える.これらの粒子をちゃんと容器の中に収まっているように抑えつけておく為には,それらの一つ一つが飛んで来るたびに跳ね返さないといけない.その為に必要な単位面積あたりの力が圧力だという理屈だ.
気体を詰めた容器の内壁には,一体どれくらいの粒子が当たっているのだろう.議論を分かり易くするため,容器は直方体だとしておこう.この中には,単一種類の理想気体が合計個入っているとする.軽々しく
個なんて言っているが,
というのはアボガドロ数と比較できるほどの巨大な数字である.
まずは容器の方向の壁のごく一部,微小面積
だけを考え,一定時間内にその部分にぶつかる粒子の数を見積もってやる.ちょっと図を描いてやろう.
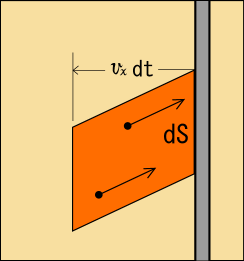
速度を持つような粒子が図に描いたような領域内にいれば,
秒以内に面積
の的にぶつかることが分かるだろう.この領域というのは,壁の微小面積
を距離
だけ移動させた軌跡の部分を表しているのである.だからこの領域の体積
は次のように表される.
ここまでの話で
秒というのは極めて短い時間であるとしておく.もし長い時間を考えてしまうと,一度
の部分にぶつかった粒子がどこか別の場所に跳ね返って,時間内に何度も同じ部分にぶつかってくる可能性も考えないといけないからだ.短い時間に限定しておけば,問題は避けられるだろう.
では,この領域内には粒子は幾つくらいあるだろうか.容器の全体積をだとすると,粒子密度は
である.だからこの体積内には
個の粒子があると計算できる.しかしその中には色んな速度を持った粒子が含まれており,今考えているような速度
を持った粒子というのは,その一部に過ぎない.その個数を見積もるには,マクスウェルの速度分布を考えて,速度に幅を持たせて考えないといけないだろう.
要するに,秒間に,微小面積
に衝突する,速度
の範囲にある粒子の数は,
と表されるということである.何だかややこしい式になってきたなぁ.
ところで,この壁にぶつかった一つの粒子は,速度の成分だけが
から
へと変化することになるので,一つの粒子あたり,
の運動量変化があったことになる.壁が粒子に力を及ぼして粒子の運動量を変化させたと見ることが出来る.壁には多数の粒子が当たっており,合計ではどれだけの運動量変化を支えていることになるのだろうか.
この微小面積を叩く全ての粒子が受ける運動量変化の合計というのは,(1) 式にを掛けたものを,あらゆる速度について積分してやれば求められることになるだろう.ただし,
の負の方向へ向う粒子はこの壁には当たらないので,除外してやらないといけない.その為に
成分の積分範囲だけは正の範囲に限っておいてやれば良い.
やれやれ,すっきりした形に落ち着いて一安心だ.さて,力というのは運動量の時間変化率のことだから,この結果を
で割ってやったものは,微小面積
に加わっている力であると考えられる.そしてそれをさらにこの面積
で割ってやったものは,この面に加わる圧力
であると考えられる.
ここまでは
方向の面についてだけ考えたが,他の面についても同じ議論をすればいいだけであり,同じ結果となるだろう.よって,ここで導かれた
というのは,方向に関係なく,容器内にある理想気体の圧力を表しているものだと考えて良い.
良く見ると,この式には圧力と体積
が含まれているではないか.これを次のように変形してやれば,熱力学との接点が見えてきそうだ.
いや,それを調べる前にちょっと待てよ.今回の最初の方で,次のような関係があるのを導き出したのだった.
右辺には共通する部分があり過ぎる.つまりこれは,次のような関係があることを意味するのではないだろうか.
これは理想気体についてだけ成り立つ式で,「ベルヌーイの関係式」と呼ばれている.流体力学にもベルヌーイの式というのが出て来るが別物なので注意しよう.一応,両方とも同一人物による業績ではある.ベルヌーイは気体分子運動論の先駆者でもあったのだ.この関係式は熱力学からは導けない式であり,気体の分子運動論によってのみ導かれるのである.
ベルヌーイはマクスウェルより 1 世紀前の人であり,彼の時代にはまだマクスウェル分布というものは知られていなかった.ではベルヌーイはどうやってこの関係を導き出したかと言うと,分子運動の平均速度という概念を使って,「厳密ではないが多分正しいだろう」と思える推論をしたわけだ.私はそれよりは,もう少しだけ正確な議論をしたかったので,歴史の順序を無視してマクスウェル分布から説明したのである.
定数 b の正体
では熱力学との繋がりを見るとしよう.熱力学によれば,理想気体には次のような状態方程式が成り立つのだった.
これは
モルの気体についての式である.
モルの気体に含まれる分子数
は,アボガドロ数を
で表すと,
個だということになる.だから,(2) 式をこの状態方程式と比較してやるためには,
にこの値を代入してやる必要がある.
その結果,次の関係があることが分かる.
よっしゃあッ!!これで今までずっと謎だった定数
の意味がようやく決定できそうだぞ.その前に,モル数とかアボガドロ数とかいう化学的な量との関わりはなるべく排除しておいてやりたいので,次のような定数
を新たに導入しておこう.
これを「ボルツマン定数」と呼ぶ.これを使えば先ほどの式は少しだけすっきりして,
と表せることが分かる.めでたい事なので,この結果を代入した形のマクスウェル分布の式を,ここに紹介し直しておこう.まず,「速度分布」は,
であり,「速さの分布」は,
である.これらを使えば色々と物理的考察をして遊べそうだが,それは次回にまわしてゆっくり楽しむ事にしよう.その前に,一つだけ補足しておきたい事がある.
ボルツマン定数
ボルツマン定数というのは,気体定数をアボガドロ数で割っただけの値である.単純に見れば,ただそれだけのことに思えるだろう.物理学者はわざわざそんなものを導入するほど,化学を敵対視しているというのだろうか.いや,そうじゃない.この定数にはそれ以上の物理的な意味が隠されている事がこれから徐々に明らかになるのである.
ボルツマン定数を使うと,理想気体の状態方程式を次のように変形する事が出来る.
モル数
を使う代わりに,全分子数
を使った式が立てられるようになる.そもそも気体定数
というのは,1 モルという,「人間が化学薬品をグラム単位で測って実験するのに便利な量」を特別視したために出てきた数値であり,そのような人為的な決まり事から解き放たれたこの定数
にはもっと根本的な意味が見出せそうなのだ.
上で出てきたベルヌーイの関係式を使えば,
という関係が見出せて,どうやら
はエネルギーと温度の関係を表す定数だと言えそうである.次のように変形してみせた方がもっと分かり易い.
温度が上がるほど,それに比例してエネルギーが上がる.へぇ,なるほど.まぁ,確かにそんな気がする.熱力学でも,理想気体の温度は内部エネルギーのみによって決まる,という議論があった.
この他に,粒子数が増えるほどエネルギーが上がる,ということも読み取れる.いや,この表現にはちょっと違和感があるかな.エネルギーは他から貰わないといけないから,ただ粒子を増やしただけで勝手に増えるようなものじゃない.だから,こう言った方がいいだろう.エネルギーが一定なら,粒子が増えるほど温度が下がる,という感じだ.
では,この 3/2 という数字は何なのだろう?この先でやることを少しだけつまみ食いしておくと,どうやら,一定のエネルギーを分かち合って安定している集団というのは,なぜか 1 自由度あたり,平均してずつのエネルギーを持つようになるらしいのである.理想気体の場合だと,一つの分子が 3 つの方向へ自由に運動できるから,3 つの自由度がある.それで
個の粒子全体としては
の自由度を持つと言える.それで,こういう式が実現しているというわけだ.
それならではなく,
を定数とした方がいいのではないだろうか?いや,ボルツマン定数にはもっと深いものが読み取れるのである.なぜ今話したようなことが成り立っているのかについて,これからさらに統計的な分析を続けることで,解き明かして行く事にしよう.










