まずは普通のスターリングの公式
統計力学では良く階乗の計算が出てくる.それが『アボガドロ数程度の大きさの整数』の階乗だったりするものだから,定義に従って具体的な値を算出するのは不可能であるし,もう桁が幾つか違っていてもどうでもいいやと思えるほどに大き過ぎる値となるだろう.
これをそのまま使っていたのでは式変形をしていくことが無理なので,別の変形しやすい形で表しておいた方が良い.そこで利用されるのが,「スターリングの公式」と呼ばれる次のような近似公式である.
あるいはこれと全く同じ意味だが,次のように書いてもいい.
これを求めるのは非常に簡単である.まず,
の対数を取ったものは次のように表せるだろう.
この右辺の値の意味するものを図で表してやろう.次のように,幅が 1 であるような帯グラフを描いてやれば,その帯の面積の合計が,その値を表していることになる.
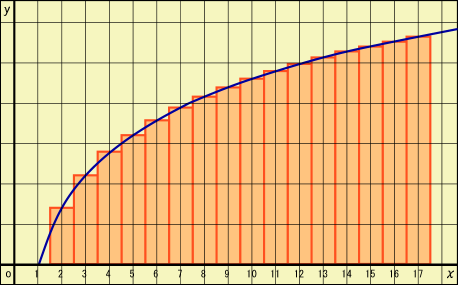
この図に描かれた曲線はを表しており,帯グラフを描く参考のために引いてみたものである.しかし良く考えてみれば,この曲線の関数を積分したものは,帯の合計の面積に非常に近いものとなるではないか.
の積分をするためには,
と考えて部分積分を使ってやればいいのだ.それで次のような計算ができる.
積分範囲についてはあまり細かいことを気にしてはいけない.どうせ
が大きくなれば,両端のわずかな差は気にならない程度となるのだから.
上の式の定数部分やなどは
が大きくなれば無視できる程度になるので,これらを省いてやれば
となり,(2) 式が出来上がるというわけだ.
精度の検証
かなり大雑把に項を省いたりしたので,この近似式の精度がどの程度信頼して良いものなのか気にしないではいられないだろう.それで次のような表を作ってみた.
| n | n ! | (n/e)n | 誤差( 比 ) |
| 5 | 120 | 21.06 | 5.7倍 |
| 10 | 3.63 × 106 | 4.54 × 105 | 8.0倍 |
| 15 | 1.31 × 1012 | 1.34 × 1011 | 9.8倍 |
| 20 | 2.43 × 1018 | 2.16 × 1017 | 11.3倍 |
| 100 | 9.33 × 10157 | 3.7 × 10156 | 25.2倍 |
最初は誤差をパーセントで表示してやろうと思っていたが,実際にやってみたらパーセントで表すことが意味の無いほどに数値に開きがあることが分かった.n が大きくなるほどに差が減っていくのかと思ったが,予想に反してどんどん増えていくし,しかも何十倍もの差がある.それでもこのどんどん増える桁数に比べれば十分に近い値を保って追随しているのだと,・・・ちょっと言いにくいが,まぁ言えないことはない.
が増えるほど誤差が減って行くだろうと予想したのは先ほどのグラフを見て考えたせいだ.グラフは対数を取ったものだったので,対数で比較してみるのが筋というものだろう.それで次のような表を作ってみた.
| n | loge(n !) | loge (n/e)n | 誤差( % ) |
| 5 | 4.79 | 3.05 | 36.3 |
| 10 | 15.1 | 13.0 | 13.8 |
| 15 | 27.9 | 25.6 | 8.2 |
| 20 | 42.3 | 39.9 | 5.7 |
| 100 | 363.7 | 360.5 | 0.9 |
こうして見ると,が大きくなるにつれて急速に真の値に近付いているのが分かる.この僅かな誤差が,対数を外した時には大きく出てしまうのだ.
どちらにせよ,この近似はこれくらいのものなのだというのを感覚的に把握した上で使うことが大切であると思う.
精度の高いスターリングの公式
上で説明した公式は普通に使うにはあまり問題はない精度があるのだが,場合によってはもっと高い精度で成り立つ式が必要となることもある.そういうときには次のような式を使う.
あるいはこれと全く同じ意味だが,次のように書いてもいい.
が一体どこから出てくるのか,と思うかも知れないが,これを求めるのは,そんなに難しい考察が要るわけではない.(1) (2) 式を求めるときに無視した部分を省かないで考慮に入れてやればいい.つまり,定数部分を
と置いて,
としてやると,
は,
と書ける.ここで
が無限大に近付くときのことを考えてやると,
であるし,自然対数の底
の定義が
であることから,
が言えるので,これら (6) (7) 式を (5) 式に適用してやって,
という形になる.(1) 式では 定数
と
という要素が抜けていたというわけだ.
あとは,なぜ定数が
になるかというところを説明すれば終わりだが,ここで天下りで申し訳ないのだが,「ウォリスの公式」と呼ばれる次の式を使う.
この式に (8) 式を代入してやれば
はうまい具合に全部消えてしまって,結局
であることが分かるというわけだ.
精度の検証
これについても精度を調べておこう.
| n | n ! | (3)式右辺 | 誤差( 比 ) |
| 5 | 120 | 118 | 0.98倍 |
| 10 | 3.63 × 106 | 3.60 × 106 | 0.991倍 |
| 15 | 1.31 × 1012 | 1.30 × 1012 | 0.994倍 |
| 20 | 2.43 × 1018 | 2.42 × 1018 | 0.996倍 |
| 100 | 9.33 × 10157 | 9.32 × 10157 | 0.999倍 |
なんと!こちらは,初めからほぼ正確であるばかりか,の増加に伴って,より正確さを増して行くのである.対数を取ったものは当然正確だろうが,一応まとめたものを書いておく.
| n | loge(n !) | (4)式右辺 | 誤差( % ) |
| 5 | 4.79 | 4.77 | 0.35 |
| 10 | 15.1 | 15.1 | 0.05 |
| 15 | 27.9 | 27.9 | 0.02 |
| 20 | 42.3 | 42.3 | 0.01 |
| 100 | 363.7 | 363.7 | 0.0003 |
申し分の無い正確さである.これに手を加えたさらに正確な公式もまだあるのだが,ここでやる必要もないだろう.











自分の言葉で書いてみる。