統計力学：ガンマ関数

ガンマ関数とは何か

高校ではの階乗,すなわちというのを習う.は非負整数だった.ガンマ関数というのはこのに整数以外を入れたら幾つになるかを表す関数である.

この関数の存在を初めて知ったとき,私はとても驚いた.階乗の定義からして,が整数以外の場合のことなんて考える意味があるのだろうか,と.例えば 2.5 の階乗 (2.5)! は幾つになるだろう？ 2.5×1.5×0.5×… と,1 ずつ減らして掛けて行くとして,あれ？この次は何を掛けたらいいのだろうか.実はその答えは (2.5)!=2.5×1.5×0.5×√π ≒ 3.32 なのだと聞かされれば,えー！？一体どういう理屈でそうなるの？と聞きたくなる.

こんな奇妙な関数を何のために使う必要があるのだろう.まぁ世の中にはこの関数の使い道も色々とあるのだろうが,私が今これを書いている理由はこの次に説明しようとしている「n 次元球の体積」という,抽象的なものを求めるためである.「世の中にはそんな関数がありますから,興味のある方は数学書を探して下さい」というのでは読者も気になって仕方ないだろうし,本当に好きでもない限り,実際に数学書を探して調べるのはかなり骨が折れるだろう.

本当は数学書を調べるよりも,物理数学の参考書や統計力学の教科書の後ろの方に付録として付いている解説を探したりする方が説明が軽くて分かり易いのだが,どの本にでも載っているとは限らない.それで,私自身の復習も兼ねて,私が満足する程度に調べて解説してしまおうと思った次第である.

ガンマ関数の性質

まず,ガンマ関数と正の整数の階乗との関係は次のようになっている. 1 だけずれているのがいやらしいが,こんなところで文句を言っても仕方あるまい.何か,生まれや定義や使い勝手に事情があるのだろう.さらに正の実数 x>0 について次のような性質がある. しかし x=0 ではこの関係は成り立たない.右辺が 0 になってしまって (1) 式と合わないから x=0 を除外するのである.代わりにが成り立つとしておく.(1) (2) (3) 式を見比べれば,ガンマ関数が階乗の素直な拡張になっていることを認めることが出来るだろう.

すると後は,この性質を満たす関数が,具体的にどのように定義されていて,どのようなグラフになっているかという点が気になるところだ.

ガンマ関数の定義

ガンマ関数の x>0 における定義は次の通りである. これを使えば, であるし,(4) 式を部分積分することにより, x>1 でとなり,(2) 式が成り立っていることが確認できる.

実は (2) (3) 式の条件を満たす関数は (4) 式の定義以外にも幾らでもあるらしいのだが,正の実軸上で対数凸である有理型関数という条件ではこの形しかないことが証明されているそうである.その意義は私には良く分からないが,やたらとくねくねしていないということだろうか.

最初の疑問への答

ここまで来れば,冒頭の疑問にも答えることが出来る.本当は (2.5)! なんて,整数以外についての階乗を書くのは正しくないことだが,これは Γ(3.5) のことであり, のように続く. Γ(0.5) については, t=x^2 の変数変換を使うことで, と計算することができる.最後の段階で,「良く使う積分公式」の中で説明した (1) 式を利用した.

Γ(4.5) や Γ(5.5) なんかもこれと同じ要領で計算できる.それを一般化した次の公式は良く使うのでついでに書いておこう.

複素数への拡張

残りは今回の目的とはあまり関係ないのでざっと説明するだけにしておこう.

先ほどの (4) 式による定義はなぜ x>0 の場合にだけ適用されるのだろうか.ぱっと見では何の問題もなさそうなのだが, x≦0 では積分が発散してしまって使えないのである.他方, x>0 の場合には収束することが証明できるが,それも際どい部分があったりして少々面倒である.

(4) 式による定義は,実部が正であるような複素数に対してもそのまま拡張できる.ところが実部が負であるような複素数にはやはり適用できない.そこで,(4) 式とは別の形式による定義を使う. この定義は実部が正の複素数の範囲で (4) 式と同じ関数になっていることが証明できる.それどころか,実部が負である領域にまで適用することができる.ただ,これでも実軸上の負の整数でだけは発散してしまうことになるのだが,これは受け入れざるを得ない.複素関数論の論理（解析接続）によって,これ以外の形の関数はありえないことが証明できるからである.

それで,実軸上でのガンマ関数のグラフは次のようになる.

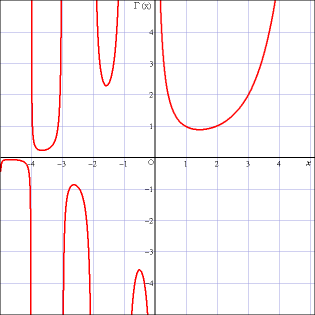
精密に計算するのが難しかったので,適当にごまかしてある.その程度のものだと思って眺めてほしい.