素粒子論：粒子の崩壊確率

いい実例がないけど大丈夫

粒子どうしの衝突の確率が理解できるようになると,粒子の崩壊確率も簡単に理解できるようになる.ほとんど同じ理屈を使い回すだけで済むからである.忘れないうちにそこまでやっておこう.忘れた人は少し前の「衝突実験の物理的解釈」という記事を参考にして欲しい.

衝突の場合とは違って,初期状態として 1 個の粒子を考える.そして,終状態としてどんな粒子が存在する状態になっているかを考えて,S 行列の振幅を求めてやるのである.また一から計算し直しかと嘆く必要はない.我々はファインマン図を描きさえすればどんな計算をしたらいいかが分かるという,思い切り手間を省くことの出来るルールを得たのだった.

ただし,まだスカラー場しか試していないので,過信は禁物である.スピノル場の場合にはもう少し違うルールが加わることになる.あとでちゃんとまとめる予定である.

4乗理論での 1 次の摂動は次のような図で表されるのだった.

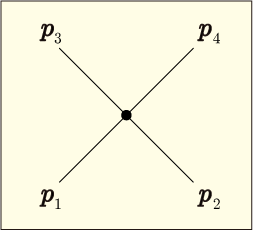
この図を少しいじって次のように変えてみよう.

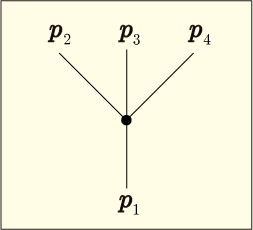
1つの粒子が3つの粒子へと崩壊して飛び去る過程を表すφ4乗理論の1次摂動のファインマン図

このように変えたものを考えても,結局は先ほどの図形の場合とほとんど同じ計算を行うだけである.

しかし残念ながらこのような反応は起きてくれない.これは 1 つの粒子が分裂して,元々の粒子と同じ質量の粒子が 3 つ出てくるという反応であり,エネルギーが全く足りないからである.エネルギー保存則を表すデルタ関数によって確率は 0 だという結果になるので,理論上は少しも矛盾はない.よって,このような図形を考えてみること自体は何の問題もない.

この反応は実際には起きないけれども,もしエネルギー的に問題がなかったならば,どんな解釈でどう計算してどんな結果が得られるかというのを考えるのは難しくはない.想像を膨らませて考えてみて欲しい.

本当は実際に起きるような例で説明してみたかったのだが,重い粒子が複数の軽い粒子へと変化する場合にしかエネルギー保存を満たせないので,単純な例が見当たらなかったのである.散乱確率についてだけ説明してあって崩壊確率には少しも触れていない教科書が意外に多いのはそのせいだろう.

エネルギー保存だけでなく運動量保存を満たすことも大切である.1 個の光子がいきなり電子と陽電子に分かれることはないし,等速直線運動をしていた 1 個の電子が突然に 1 個の光子を放つことも起きない.だからあとちょっと先を勉強して電子や光子の相互作用を知ったくらいではまだ崩壊のいい実例に辿り着けない.β崩壊などを例にすればいいのかも知れないが,そこまでやるにはまだ準備が足りないし,そこまでやらなくても現段階で理解は可能である.

導出はこんなに簡単

では,具体的にやってみよう.初期状態に 2 つ,終状態にも 2 つの粒子がある場合の散乱振幅は次のように表されるのだった. 一方,初期状態に 1 つ,終状態に 3 つの粒子がある場合の散乱振幅は次のようになる. このように,図形が同じならほとんど違いはない.エネルギー運動量保存を表すデルタ関数の中身が少し違うだけであり,不変散乱振幅の部分は同じである.これを 2 乗してやることで確率密度になる. (2π)^4 δ^4(0) の部分は全宇宙の時空の体積だと解釈できるのだったから,それで割ってやれば,単位体積,単位時間あたりでこの遷移が起こる確率密度だと解釈できる. 確率密度を確率にするためには幅を掛けてやればいい.つまり,粒子の崩壊後に現れる 3 つの粒子がそれぞれ,およそ $p_{2}$ , $p_{3}$ , $p_{4}$ の運動量を持って $dp_{2}$ , $dp_{3}$ , $dp_{4}$ という微小範囲のいずれかへと飛び散っていく微小確率は次のようになる. さて,初期状態の 1 粒子というのは,実は「個数密度 1/(2π)^3 で一様に存在している状態」だと解釈されるのだったから,これに (2π)^3 を掛けてやれば,単位体積あたり 1 個存在している状態での確率に直すことができる. 「単位体積あたりに 1 個存在している粒子が崩壊するという,単位時間,単位体積あたりの確率」ということは,もはや体積や個数密度などは何の関係もなくて,1 個の粒子が単位時間内に崩壊する確率だと言えるだろう.これが今回の結論とも言える式である.

崩壊後に飛び散る粒子のエネルギーや方向に興味がなければ,この式をそれぞれの運動量で積分してやればいい.単位時間内に崩壊が起こる確率を得ることができる.

相対論的な時間短縮の効果

さて,初期状態の粒子が静止していれば $ω(p_{1})=m$ であるから, と表すことが出来る.場の理論が表す相互作用というものに対して何かダイナミックなイメージを持っていたのに,静止していた粒子が勝手に崩壊する確率までもが同じ理論で説明できてしまうのが驚きだ.

このように,素粒子の反応というのは粒子と粒子がガンガンぶつかって起きるようなイメージではなく,ただ,現状から許される別の状態に向かって,確率的に変化するというイメージのものであるらしい.

ところで,粒子が動いているかどうかによって崩壊確率が変わってしまうというのが少し奇妙な気がしてくる.素早く動いているほど分母の値が大きくなって,崩壊確率が下がるらしいのである.なぜそんなことが起きるのだろうか？ひとまず,どれくらい下がるものなのか,静止しているときと動いているときの比を計算してみよう. ああ,これは……！動いている相手の時間がゆっくりになって見えるという相対論的効果の式と同じだ.時間がゆっくり流れていれば,それと同じ割合で,一定時間内に崩壊する確率が下がる.(1) 式の分母に $ω(k_{1})$ が入っているというごく単純な形でありながら,たったそれだけで相対論的効果までもが正しく言い表されているのだ.

ちなみに,(1) 式を積分して得られる確率についても,この結果は変わらない. $ω(k_{1})$ の部分は積分される変数とは関係ないからである.

あと,(1) 式も (2) 式も,流儀によって違いがなくちゃんと同じ形の結果になるので安心して欲しい.いつの間に合流したのだろうと不思議に思えるかもしれないが,散乱振幅が求まった時点でどの流儀も似た形になってきており,1 粒子状態の解釈で微調整することで完全に一致した結果となるのである.