素粒子論：相互作用項の追加

自然単位系で表した自由場

ここまでは,粒子間の相互作用がない場合の話をまとめてきた.粒子が幾つ存在していようが解として許されるというものであり,しかしながら互いに少しも反応しないので面白いことも起きないのだった.

とりあえず,自然単位系を採用してスッキリした自由場のラグランジアン密度を幾つか書いておこう.

まず電磁場（質量のない実ベクトル場）は次のようである. 電子場（スピノル場）は次のようである. 実スカラー場は次のようである. 符号が教科書と違っているかもしれないが,ミンコフスキー計量の流儀の違いのせいである.

相互作用項の具体例

相互作用がある場合についてはどう考えればいいかというと,複数の場が絡み合うような形の項をラグランジアン密度に追加すれば良いのである.

解析力学のように変分原理を使った理論体系というのは非常に強力で,複数の粒子が相互作用することによる影響をエネルギーという形でハミルトニアンに記述しておけば,それに見合った運動方程式が得られるのであった.ラグランジアン密度に手を加えればハミルトニアンにも影響し,同様な変更が可能になるだろう.

例えば電子や陽電子が,それぞれが持つ電荷によって反発したり引き合ったりする様子を表したいとする.電子も陽電子も「電子場」によってまとめて記述される.しかしこれらが電荷を介して互いに反応するためには電磁場の存在が不可欠で,ラグランジアン密度には次のように電子場と電磁場の自由場を表す項と,さらにそれぞれが絡み合う項を入れたものを考えてやることになる. このようにするだけで色んな現象が表せるようになる.電子と陽電子が対消滅して光子に変わる様子や,2 つの電子が間に光子をやり取りして,初めとは別の運動量を持つ 2 つの電子に変わって再び飛び去る様子も表せる.詳しくはあとでゆっくり説明するつもりである.

この相互作用項の中にある $\bar{ψ}γ_μ ψ$ という部分を j_μ と略記してやると,相互作用項は ej_μ A^μ のようにスッキリと表せるようになる.この j_μ のことを「電磁カレント」と呼ぶ.要するに電流のことである.

ずっと前にマクスウェル方程式を再現するためのラグランジアン密度をどう表したらいいのかと考えていたときのことを思い出して欲しい.「電磁場のラグランジアン」という記事の中の (6) 式あたりである.ラグランジアン密度に j_μ A^μ という項を付け加えることによって「電流密度が存在する場合のマクスウェル方程式」が作れるのだった.その辺りと無関係では無さそうだ.

他の場合も紹介しておこう.ミューオンというのは,質量以外は電子とよく似た性質を持つ粒子である.だから電子場と同じような形をした項を入れることでその存在を表せる.しかし電子とは別の場として導入する必要がある.もし電子とミューオンが電荷を介して力を及ぼし合う様子を計算させたければ,「電子場」と「ミューオンの場」と「電磁場」の 3 つの場をラグランジアン密度に入れてやって,さらに電子場とミューオンの場がそれぞれに電磁場とやり取りするような形の項を入れてやればいい. ミューオンの場とミューオンの質量にはダッシュを付けておいた.このようにすると,電子と陽電子が対消滅して光子となり,そこからミューオンとその反粒子が対生成されるような現象も記述できる.現実はそれほど単純ではないのだが,理論的にはそれらしいものが計算できる気がする.

この場合には電磁カレントをのように定義しておいてやれば,二つある相互作用項を ej_μ A^μ という一つの項にまとめて表すだけで済むだろう.

今回は雰囲気だけの紹介なのでこれ以上の深入りはしないが,実際はまだあれこれと改良が必要になるのである.

相互作用の形の制限

気になるのは,相互作用として追加する項をどのような形で書いたらいいかという点である.上で紹介した相互作用はどうしてそのような形になっているのだろう？

特殊相対性理論を満たしているような理論を作りたいわけだから,もちろん相互作用項についてもローレンツ変換に対して不変な形に書く必要がある.つまり,テンソルの形式で表してがスカラーになるようにしておかなければならない.

また,ゲージ変換に対する不変性も要求される.上に書いた電子場と電磁場の相互作用では,電磁場 A^μ だけにゲージ変換を施すと不変ではないが,電子場の方にも次のようなゲージ変換を施して不変性が保たれているということにしている. 実はこの電子場に対して行っているゲージ変換というのは自由場の項と相互作用の項を合わせて考えないと不変にはなっていない.電子の自由場だけではゲージ変換の不変性が成り立っていなかったということになる.まぁ,この辺りの話も色々と話し出すと面倒なので後にしておこう.今回は用語だけの軽い紹介のつもりである.

他には「大域的位相変換」をしたときの不変性というものも要求される. ゲージ変換には任意関数 χ(x,t) が使われていたのだった.これは時空の位置 (x,t) の関数になっているので場所ごとに異なる位相で変換するという意味になっている.それでゲージ変換のことを「局所的位相変換」という別名で呼ぶこともある.それに対して,上の変換で使われているは定数なので,宇宙全体で同じ位相変換をするという意味になり「大域的位相変換」と呼ぶのである.

あるいはどちらも広い意味でのゲージ変換だと考えて,「大域的位相変換」のことを「第一種ゲージ変換」と呼び,「局所的位相変換」のことを「第二種ゲージ変換」と呼ぶこともある.

実数場を考えているなら,大局的位相変換によって複素数になってしまうので,次のような単純な変換に対して不変であることだけを要求することがある. これは「Z₂不変性」と呼ばれており,Z₂ というのは群論の用語である.「位数 2 の巡回群」という意味で,典型的には 1 と -1 だけを元とするような群である.

このような様々な不変性が成り立つべきだというのはあらかじめ明らかに分かるようなものではない.先人たちの地道な試行錯誤によって,宇宙にはこのような対称性があるに違いないと絞り込まれて行ったのである.我々入門者はその結果をお借りして道理が分かるまで楽をさせてもらうことになる.基礎的な話を終えたあとでこのような議論に入っていくことにしよう.

さて,不変性の例について幾つか話したが,これだけではまだ可能性がほとんど絞られていなくて,幾らでも複雑な相互作用を考えて付け加える余地がありそうである.それらを片っ端から試してみて現実とピッタリ合うものを探す必要があるのだろうか？それとも,自然界が何らかの形の相互作用だけを採用する基準のようなものが他にも隠されていて,それを知ることでもっと絞り込むことができるのだろうか？

質量次元からの制限

とても分かりやすくてありがたい制限が他にもある.ラグランジアン密度の質量次元が 4 であったことを思い出そう.物理的な次元が合うような組み合わせで相互作用を表現する必要があるのだ.

ベクトル場とスカラー場の質量次元は 1 で,スピノル場は 3/2 であった.また ∂^μ や ∂_μ も 1 だった.これらを組み合わせて 4 になるようにすればいい.足りなければ質量次元を持つ物理量をや m^2 のような形の定数パラメータとして混ぜ込んでおけばいい.これで,相互作用項として許されるパターンはかなり限定されるだろう.

いや,それなら,質量次元が負になるような定数パラメータを混ぜ込んでやれば幾らでも複雑なパターンが許されるのではなかろうか？ところがありがたいことに,そのような複雑な項は「繰り込み理論」の観点からあまり望ましくないということが分かっているのである.

繰り込み理論はずっと後の方で説明する予定だが,私もまだしっかり理解していないので紹介程度に話しておこう.このあと,何の工夫もなく普通に計算してやると計算結果が無限大に発散するという困難に悩まされることになる.初期の場の理論が全く使い物にならないと思われたのはこの困難のせいでもあった.ところが,ちょっとラグランジアン密度の形に手を加えて無限大と無限大を打ち消し合うようにしてやって,その差が現実の物理量を意味していると解釈して実験値を代入してやると困難が回避できるのである.

質量次元が負のパラメータを含む項があると,このような工夫を行うために無限個のパラメータを混ぜ込まなくてはならなくなってしまうようである.無限個のパラメータを調整する必要がある理論というのは信用しにくいし,あまり嬉しいものではない.

また,場の理論というのは,あるエネルギーより低いところで成り立つ近似的な理論（低エネルギー有効理論）だと考えられそうである.その場合,そのエネルギーよりずっと低い領域では,そのような複雑な項からの寄与は他の項に比べて無視できるほど小さいという見通しもある.そういうわけで,とりあえず正の質量次元を持つパラメータだけを使って質量次元を 4 にするように項を作ってやれば良いようである.

自己相互作用

さて,ここまで,相互作用項というのは複数の場を絡み合わせる形にしなければならないかのような説明をしてきた.ところが例えば実スカラー場の場合,次のように相互作用項を追加してやると「自己相互作用」が起きるのである. 複数の実スカラー粒子どうしが,他の場の助けなしに運動量を交換し合って,初めとは異なる運動量の粒子として飛び去ることになる.実スカラー粒子どうしで直に衝突すると表現してもいい.これは「4乗理論」と呼ばれており,考える場も 1 種類だけでいいし,スカラー粒子だから複雑な要素がほとんどないというので,具体的な計算の最初の例としてよく使われる.

係数として入っている 1/4! というのは,計算を進めていくとうまく消えるように入っているもので今は気にする必要はない.は相互作用の大きさを表す無次元のパラメータである.確かに質量次元は 4 になっている.

なぜ 4 乗なのか？3 乗や 2 乗ではダメなのか？ちゃんと理由がある.2 乗は,すでに自由場の式に出てきており,質量の大きさが変わるだけの効果しかない.1 乗や 3 乗は先ほど「Z₂不変性」の話で出てきた場の符号を変える変換をしたときにラグランジアン密度の形が変わってしまうから却下である.

初歩的な教科書ではこういう理論の背景を知らされないまま,いきなりこのような形の相互作用項を見せられて計算が始まったりする.いや,素直に始まれば良い方で,計算を進めるために必要になる定理や,予備的な計算の説明が長々と続いたりするのである.それで何をやっているかさっぱり分からず,置いてきぼりな気分を味わう.すると入門者は思うのである.「こんな,いかにも例題のために試しに作ってみたような嘘っぽい相互作用ではなく,さっさと量子電磁力学のような「現実に起きている」本物の相互作用について教えてくださいよ！」と.しかし決して使い捨ての例題というわけでもないのである.

この相互作用もファインマン図で描けるのだが,初学者があちこちの啓蒙書で見て憧れを抱いてきたようなファインマン図とは似ても似つかない.

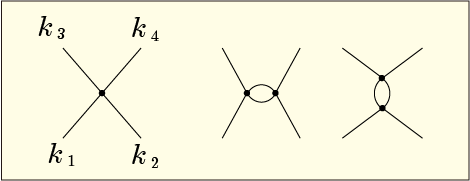
これは一例だが,一番左の図はもっとも単純な 1 次の摂動を表したもので,運動量 $k_{1}$ と $k_{2}$ の入射粒子が反応して $k_{3}$ と $k_{4}$ となって出ていく様子を表している.他の図は,2 次の摂動の一例であるが,直線で結べないので仕方なく曲線を使っている.

ファインマン図では電子などのスピノル場を実線で,光子などのベクトル場を波線で,パイオンなどのスカラー場を点線で表すという習慣があり,上のような図も教科書によっては点線で描かれていることがある.それほど厳密なルールではないので,実線のことが多いかもしれない.それで「自分は一体どんなマイナーな独自理論を学ばされているのだろう？知りたいのはこんなことではないのに」という不満でいっぱいになってしまうのである.

カンフー映画などにありがちな展開だ.退屈な修行を毎日毎日やらされて,師匠は一体いつになったら本当の技を教えてくれるのだろうと不満をためて一度は逃げ出すわけだが,実は初めから本物の技を教えてくれようとしていたと気付くというオチである.