タピオカが飲めるのも大気圧のお陰
ストローを吸えば,飲み物が上がってきて,飲める.当たり前だ.誰もそれが大気圧のお陰だなどと思いもしない.それほどまでに当たり前の現象だと思われているから存在を見逃されてしまう.そこが怖いのだ.
ストローを吸うとき,本当は何が起こっているのかを説明しよう.ストロー内の空気を吸い込むと,空気の量が減ってストロー内の圧力が下がる.ストロー内部の空気は以前は外部の大気圧と同じだったが,もはやストロー内部では飲み物の表面に強い圧力を掛けられなくなっている.ストロー外部の飲み物の表面には常に大気圧が掛かっており,その圧力に負けて,ストロー内部を飲み物がせり上がってくる,というわけだ.
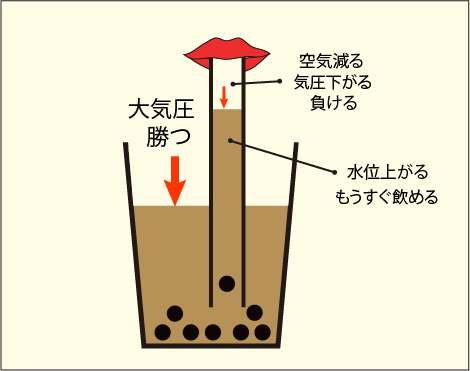
大気圧が持ち上げることのできる飲み物の高さにも限界がある.前回,標高 0 m での平均大気圧は約 10 m の水圧と同じくらいだという話をしたのを覚えているだろう.つまり,大気圧は,10 m ほどの水の重みを支えることしかできない.もしストローを思い切り長くして思い切り空気を吸い込んだとしても,飲み物は 10 m ちょっとの高さまでしか上がってこないのである.ストロー内部が完全に真空になるほど吸い切ったとしてもだ.
ストロー内部が真空になるとストロー自体が大気圧に負けて潰れてしまうので,これを実際に試したければ金属製のストローを使う必要があるだろう.
どうやら人間が吸う力では 6 m くらいが限界のようである.
10 m 以上のストローというのは非現実的な話だが,実はもっと現実的な話がある.10 m 以上の深さの井戸水をポンプで汲み上げることができないことは大昔から知られているのだ.これは炭坑でも問題になっており,深く掘った坑道に次々と溜まってくる水を汲み上げる際に面倒な制限となっていた.10 m ごとに水桶を用意して,多段式にする必要がある.神様,どうせ結局は吸い上げさせてくれるんでしょ?少しくらいずるさせてよ?と言いたくなる.
トリチェリの実験
イタリアの物理学者トリチェリはガリレオ・ガリレイの弟子であった.ニュートンより前の人である.
彼はポンプで 10 m 以上の水を汲み上げることができないという問題を説明するために,次のような実験を行った.1643年のことである.
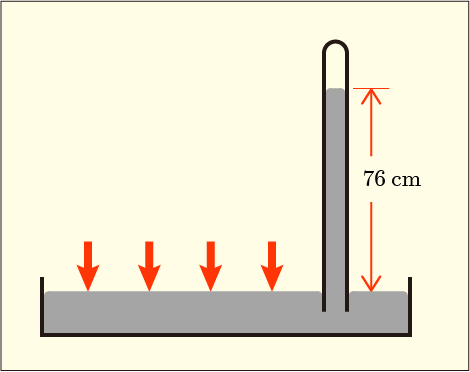
ガラス管の中を,少しも空気が入らないように水銀だけで満たしてやって,その後で逆さまにして水銀の入った容器の中で立ててやる.すると,水銀というのは密度が鉄の 1.7 倍くらいもあって,かなり重いので,ガラス管の中にあった水銀の一部は容器の中へ流れ落ちてきてしまう.しかし全て流れ落ちてしまうわけではなく,容器内の水銀の上面から約 76 cm ほどの高さで止まる.その高さまでは一気に落ちてくるのである.出ていった代わりに空気が入るわけではない.そのような隙間はどこにもない.ガラス管の上部には何もない真空が現れるのである!
ガラス管を傾けてみても同じ高さが維持されて,それより上には上がってこれない.なぜこの高さなのか?大気が液面を押す圧力と,液面より上にある水銀の重みによる圧力がちょうど釣り合っているのだと考えればいいのではないだろうか.そういう問題提起をした実験である.
この約 76 cm というのを計算で求めてみよう.ガラス管の断面積をとすると,高さ
までの水銀の体積は
である.水銀の密度を
とすると,ガラス管内の水銀の質量は
であり,これに重力が掛かるから,下方に掛かる力は
である.面積
で割ってやれば圧力は
であると分かる.これが大気圧
と釣り合ってこの状態が維持されていると考えれば
が成り立つ.つまり高さは次の式で求められる.
確かに約 76 cm が得られる.
ところで,このガラス管の上部にできる空間は真空だと言ったが,実際は希薄な水銀の蒸気で満たされている.水銀の原子は激しく熱運動していて液体表面から原子が飛び出したり戻ってきたりというのを絶えず繰り返しているので,水銀蒸気が満たされた状態がほぼ一瞬で実現して安定する.しかし水銀の蒸気圧は 315 K (約42℃) で 1 Pa しかないし,温度が下がれば急激に下るので,常温付近ではもっとずっと低いだろう.大気圧が 10 万 Pa 程度あるのに対して,1 Pa 以下であるから,これくらいならほぼ真空と言い切ってしまってもなんら問題ないほどである.
水の場合にはどうなるか
水銀は密度が高いので 76 cm 程度しか持ち上がらないが,水を使って同じ実験をやったとしたらどれくらいの高さになるだろうか.水の密度は 25 ℃で 997 kg/m3 だそうだからそれを使って計算してみよう.
確かに 10 m ほどになる.井戸水が汲み上げられないことにも説明が付く.
ただし,水の場合には水銀とは少し違う部分が出てくる.蒸気圧が無視できないほど高いのである.20 ℃における水の蒸気圧は約 23 hPa である.これは水温が高くなるほど高くなり,100℃では 1013 hPa にもなるから大気中でも沸騰するのである.
気圧が下がると水は低い温度で沸騰すると聞いたことがあるだろう.真空になれば勝手に沸騰する.科学館などでそういう展示があるが,あれは空気を抜き続けるから沸騰が続くのであって,このトリチェリの実験を水で行った場合には,おそらく一瞬で真空が蒸気で満たされて安定するだろう.一瞬で収まるとはいえ,結果としてガラス管内に生じたままになっているこの約 23 hPa の圧力は無視できない.
このように,20 cm 近くも打ち消す効果があるのである.気温が上がるほどガラス管内の蒸気圧が高まるので,同じ外気圧であってもその分だけ水位は低くなるだろう.
ここでの計算は説明を略したが,蒸気圧 23 hPa と水の重量による圧力の合計が大気圧 1013 hPa と釣り合うと考えて計算して,水の水位を求めた方が意味が分かりやすいかもしれない.10.36 m より 0.23 m だけ低い数値が求まるだろう.どちらの計算も等価である.
マクデブルクの半球
ドイツの物理学者ゲーリケはトリチェリと同時代の人であった.彼は大気圧や真空についての研究をしており,ピストン式の真空ポンプを発明していた.他に静電気の研究もしている.
彼はポンプを使って作り出した真空状態が不思議な吸引力を持つことに気付き,次のような実験をした.直径 50 cm ほどの銅製の半球を二つ合わせて球にして,真空ポンプで内部の空気を抜く.こうすると二つの半球は吸い付き,ちょっとやそっとの力では離れない.多数の馬を使って両側から引いたところ,大音響とともにやっとのことで引き離すことができたというのである.ゲーリケがマクデブルクの市長であったときに行った実験なので「マクデブルクの半球」と呼ばれている.
……とまぁ,そういう説明が多いわけだが,文献によって実験の細部が微妙に違っている.よくよく調べてみると,彼は少なくとも3回ほど,似たような実験を行っているのである.
最初は1654年,神聖ローマ帝国議会において,神聖ローマ皇帝フェルディナンド3世の御前で.この時は15頭ずつ,計30頭の馬を使っても引き離すことが出来ず,半球に付けたバルブを軽くひねって空気を入れると容易に引き離せるという筋書きだったようである.
次は1656年か1657年,地元のマクデブルクにて.この時は8頭ずつ,計16頭の馬を使って引き剥がすことに成功している.というか,実験ショーのようなものなので,筋書きを変えたのだろう.このときの実験が書物として広まったので有名になったようである.
さらに1663年か1661年頃,ロンドンにて,ブランデンブルク選帝侯の御前でも同様の実験を行っている.この時は12頭ずつ計24頭の馬を使って引き剥がした.
ゲーリケは1646年から30年近くも市長の地位にあったので,いずれの実験も市長として行ったわけである.科学的な実証実験というよりも,政治的な場で行われた見世物的なものであることが分かる.ということは,これ以外にも事前に予備実験を行ったりして失敗のないように調整したに違いない.すると気になるのは,彼はなぜたびたび,各地で地位の高い人々の前でこのようなショーを行ったのだろうか,という点だ.
実は彼は物理学者である前に優秀な政治家であり,その余暇として物理の研究をしていたのである.この時代には物理というのはそのような人々によって行われるのが普通だった.彼の業績を調べるとなかなか面白い.政治的地位と科学的な知識を利用して三十年戦争の傷跡から街を復興させたのである.マクデブルクの市庁舎に 10 m の水圧計を設置し,気圧を測って嵐の到来を予報したりもしている.魔術師的な振る舞いは政治的な支持を集めるのに助けになったであろう.
トリチェリの実験の方が 10 年以上先に行われているのだが,ゲーリケはこの実験をしたときにはまだこの吸引力の正体を知らなかったようである.後にトリチェリの実験のことを伝え聞いて,大気圧が原因であることを理解したのだった.
当時はまだアリストテレスの「自然は真空を嫌う」という説が広く信じられていたが,この実験が有名になり,あちこちで真似されて行われるようになり,真空という状態が人工的に作ることができるものであるということが徐々に認められていったのであった.そういう意味で科学史的にはかなり重要なのである.
気圧計の豆知識
トリチェリの実験と全く同じ仕組みによって気圧を測ることができるので,長い間気圧計として利用されてきた.古い文献で「水銀柱」と言えばほとんどの場合,気圧計のことである.気圧以外の圧力も測ることができるので,例えば血圧計などで水銀柱が用いられてきた.(私の子供の頃には病院でまだ普通に使われていた.)
しかし衝撃に弱い,長い,重い,傾けるとおかしくなるなど,持ち運びに不便だというので,少々精度は落ちるが小型の機械式の圧力計も使われるようになった.アネロイド気圧計(1843)やブルドン管気圧計(1849)は18世紀中頃の発明である.
20世紀の終わり頃には気圧によってコンデンサの静電容量が変化することを利用した電子式の圧力計が使われるようになり,IC化により精度が向上した.自動計測にも都合が良いので,気象庁でも置き換えが進んでいる.
今回の記事を書いていてちょっと興味が出てきたので,お部屋のインテリアに水銀柱式の気圧計を手に入れることができるものだろうかと探してみたが,モノタロウで16万円で売っているのを見付けた.これは精密測定用のもので,インテリアとして気軽に買うようなものではない.
水銀自体はそれほど高価な物質ではないが,有毒なので取り扱いに注意が必要である.近年,水銀をなるべく環境中に排出しないようにというので,使用が制限される傾向にある.例えばEUでは2007年に発効した環境規制によって,水銀を使った製品の製造,輸出入が厳しく制限された.水銀を利用する方式の気圧計,圧力計はほとんど世の中から姿を消しつつある.
最近売られている水銀を使っているように見える体温計などは,実は水銀ではない可能性が高い.より安全な Ga,In,Snの合金(ガリンスタンという登録商標)が使われている.
もう一つ書いておいていいだろうか?水を使った 10 m を超える長さの気圧計というのは科学館などの展示のために,近年になって面白半分で作られたものだとばかり思っていた.しかし科学史を調べていくと,けっこう昔からあちこちで作られているのである.実はトリチェリ以前にも存在していたりするから驚きだ.ガラス管ではなく鉛管を使ったようである.どうやって水位を確認したのだろう?一番上だけガラス管をつなげたのかな?ほら,こんな調子で興味が止まらない.











面白くなってきりがない。