流体力学：浮力

浮力が存在する理由

流体中にある物体には上向きの力が働く.これを「浮力」と呼ぶ.

上向きと言っていることからも分かるように,今回は重力の影響を前提とした話である.パスカルの原理で重力を無視したりしていたので,わざわざこういう注意書きをしておかないといけない気分になった.

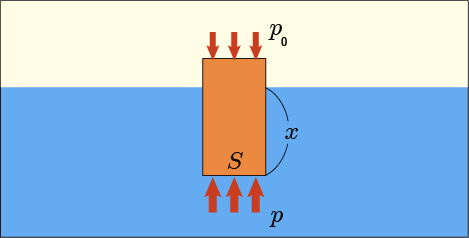
流体の種類は何でもいいのだが,とりあえず水を思い浮かべるのが身近で分かりやすい.考えやすいように,水中に直方体の物体がある場合を想定しよう.

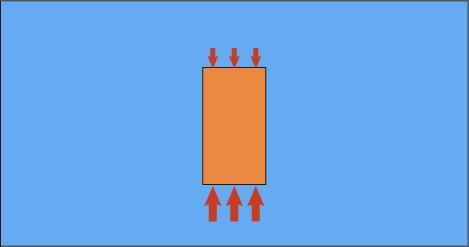
水中にある直方体の物体の下面に強い水圧がかかり、上面には弱い水圧がかかっている浮力の説明図

水の深いところほど水圧が高く,浅いところほど水圧が低いので,この物体の底面には強い上向きの力が掛かり,上面にはそれよりは少し弱い下向きの力が掛かる.合計すると上向きの力の方が少し勝つことになり,それが浮力の正体である.

浮力の大きさ

浮力の大きさを計算する方法を考えよう.水深での水圧は次の式で表されるのであった. は水の密度であり,は重力加速度である.この式は水に限ったものではない.その流体に圧縮性がほとんどない場合には,このように深さに比例する式で表されるのである.

空気などのように圧縮性が高い場合には,圧力 p が上がるに従って密度 ρ が変化してしまうのでこのような単純な形には書けないのである.

水中にある物体の底面積はで,高さはであるとする.そして上面は深さのところにあるとしよう.

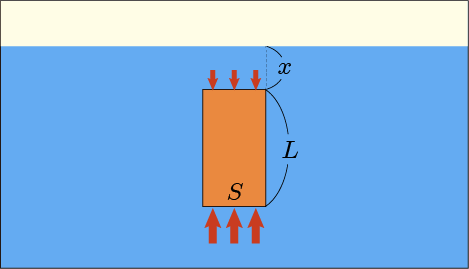
すると,上面には下向きに ρgx×S の力が働き,下面には上向きに ρg(x+L)×S の力が働くから,上向きの力を正として合計の力を計算すると次のようになる. このは直方体の体積であるから, ρLS というのがちょうど,その体積を(物体ではなく）流体が占めていた場合の,流体の質量に等しいことになる.その質量に重力加速度が掛かったものが浮力なのだから,次のように表現すれば分かりやすい.

物体が流体の中に沈められているとき,
その物体が排除した流体の重さと同じ大きさの力が,
物体に上向きに掛かっている

これは「アルキメデスの原理」としてよく知られている表現である.

どんなサイズの直方体であってもこのことは成り立つし,実は直方体だけでなく,どんな形状の物体であっても同じことが成り立つ.どんな形であろうと,細い直方体の寄木細工のように表現できて,そのような集合体だと考えればいいからである.

寄せ木細工って何だ？と思った人が検索してみてもおしゃれなものばかりで,私がイメージしたようなものは出てこないと思う.私が伝えたいイメージは,割り箸だけを使って中までぎっしりと詰まったウサギの形を表現するとか,そういうものである.現代的には「ボクセルアート」あるいは「3D ドット絵」で画像検索してもらった方が伝わりやすいかもしれない.

物体が流体そのものだったら

普通の教科書ならばこれくらいで説明は終わりなのだが,余計なことをあれこれ考えてみよう.

物体として流体そのものを考えてみる.物体が存在していなくて代わりに流体があるという状況だが,要するに流体だけしかないという状況である.その場合,流体自体には浮力が掛かっていると考えていいのかどうか？

流体には流体の重量と同じ浮力が掛かっていると考えれば,浮力と重量との合計の力は打ち消し合って 0 になる.だから流体はどちら向きの力も受けずに,その場でじっとしていられるというわけだ.このように,流体そのものにも浮力が掛かっていると考えてみても全く問題ないようだ.

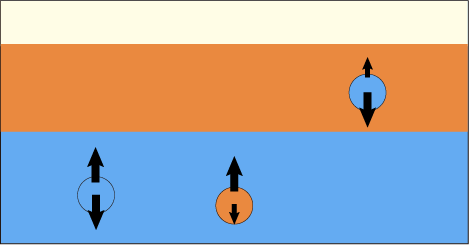
水と油を混ぜたときに起こることを想像してみよう.水の中にある油は強い浮力を受けて,油自身は軽いから,上向きの力が勝って上へ向かう.油の中にある水はそれほど強い浮力は働かなくて,水の重量はそれよりも重いから,下向きの力が勝って下へ向かう.

水の中にある水、水の中の油、油の中の水について、それぞれに重力と浮力を書き込んだ図

物体が水面に浮かんでいたら

物体が完全に水中にあるわけではなく,水面より上に一部だけ出ていたとするとどうだろうか？

例えば直方体で考えてやれば,上面には全く圧力は掛かっていないことになる.

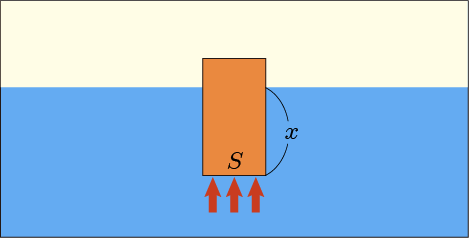
下面に掛かる深さのところの圧力だけで考えてやれば, となり,が水に浸かっている部分の体積に相当するので,やはりアルキメデスの原理の表現通りのことが成り立っていることになる.物体によって排除させられた流体の分だけの浮力が掛かるということで正しい.

いや,このときの物体の上面には大気圧が掛かっているではないか,と思うかもしれない.しかしそこまで問題にしたいのなら,実は先ほどまで使っていた水圧の式はゲージ圧力であって,実際は水中にも大気圧 $p_{0}$ が掛かっていることを思い起こす必要がある.

つまり,水中の絶対圧力は次のようになっている. この式を使ったとしても,先ほどの「物体が完全に水中にある場合」についての議論には影響が無い.というのも, $p_{0}$ の部分は水の深さに関係のない定数であるから,上面と下面とで打ち消し合って消えてしまうからである.

物体が水面から顔を出している場合についても同じである.気圧の影響は水中にまで及んでおり,上面と下面とで打ち消し合ってしまうので,気にしなくても良くなってしまう.

空気中の浮力

今の話は少し雑であった.空気中では物体の上面に大気圧 $p_{0}$ が掛かるということにしていたが,その $p_{0}$ というのは水面に掛かっている大気圧であって,水面より少し上ではもう少し圧力が低いのではないだろうか.

飛行船だって気球だって,浮力を利用して浮かんでいるのだから,水圧ほどではないにしても,高度による僅かな圧力差があるはずである.

水面から顔を出した直方体の上面に掛かる大気圧を $p_{1}$ だとしよう.

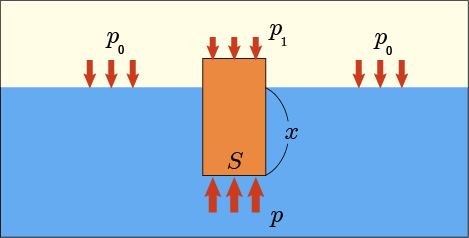
先ほどの図に水面に掛かる気圧を書き加え、物体の上面に掛かる気圧がそれよりも弱いことを表した図

水に浸かっている底面には水圧の他に $p_{0}$ が掛かっている.先ほどのように上向きの力を正として直方体に掛かる力の合計を表してみよう. 第 1 項は水に沈んだ部分について水から受ける浮力であり,第 2 項は水面より上に出ている部分が空気から受ける浮力だと解釈してもいいだろう.

さて,もう少し話を広げておきたい.水中から一部だけ顔を出しているような物体ではなく,完全に空中にあるような物体に働く浮力についても考えてみよう.それはどういう式で表せるものだろうか？

空気は圧縮性があるので,圧力が下がるほど広がって,密度が下がっていく.上空に行くほど空気は薄く,軽くなっていく.そういうわけで,水のように深さと圧力が比例する形ではなく,指数関数で表される形で上空へ行くほど圧力が減少していく.標高をとするとおおよそ次のような形になる.（導出は省略）実際には上空へ行くほど気温も変化するので,面倒くさいことに,定数が高度によって変わったりするのである.気象予報士の資格を取ろうと努力すればその辺りにも詳しくなれるであろう.

地表付近に話を限って,高度差もごく僅かだとすれば,高度 $x_{1}$ と高度 $x_{2}$ （ $x_{2}>x_{1}$ とする）の圧力差は次のように近似できる. つまり,ごく小さな範囲では圧力差は高度差に比例すると言ってもいい.しかし定数の値が分からないままである.

空気の密度がほとんど変化しないと言えるほどのわずかな高度差ならば,水圧が生じるのと同じイメージが成り立つだろうから, のような関係になっていると考えて良いだろう.そうなると空気中でもアルキメデスの原理の表現がそのまま成り立っており,「物体が排除した空気の重さと同じ大きさの浮力が働く」と考えておけば良さそうである.

もっと大きな高度差がある場合でも,このような微小な圧力差が積み重なっていると考えればいいので,結局は「物体が排除した空気の重さと同じ大きさの浮力が働く」という表現がそのまま成り立つと考えて良さそうである.

ちょっと気を付けてほしいのは,空気の密度が高度ごとにどんどん変わることを考慮する必要がある点である.言葉では簡単に表せるが,式で表そうとすると単純には書けない.

言葉で説明するより数式で書いた方がずっと簡単だということは良くあるが,今回は逆なのだな.

ご案内

前回の記事の最後の方で「オイルタンカーの真下の水圧は高いか低いか」という話を浮力まで含めて検討しようと予告していたが,書いているうちに浮力に関する雑談が増えてしまったので今回はそこまでたどり着けなかった.その他にも浮力について書きたいことがあれこれ出てきているので,それらの話は独立した雑談的な記事として流体力学の最後の方にまとめて載せていく予定である.