流体力学：パスカルの原理と重力

この原理が成り立つ理由

パスカルの原理が成り立つのはなぜなのか,と聞かれたら,どう説明するのがいいだろうか？

もしも圧力がどこもかしこも一定でなかったとしたら,容器の中の流体は圧力差によって動き続けることになるだろう.だから流体がすでに静止した状態になっているとすれば圧力が一定になっていなければおかしいのである.しかしそのような静止状態に必ず落ち着くという論理的な保証はあるだろうか？

ある,と答えよう.少しも難しくはない.どこかに少しでも圧力差があれば,「圧力差を解消」するような方向へと移動する.その結果として別の場所に新たな圧力差が生じたとしてもそれもすぐ解消されて,結果として「全体で圧力が一定」の状態を目指して動くことになるだろう.問題なさそうだ.

もっと理論的な説明が必要になるかと思って警戒していたが,自分はこの程度で納得できてしまった.どの向きにも圧力が同じになるという点については,以前の記事で三角形の図を使って説明したものが使える.任意の形の流体要素を考えたとき,それが静止するためには,どんな向きからも同じ大きさの圧力が掛かっていないといけないのだった.その説明の中で,接線応力が働かないということを仮定として使ったのだった.パスカルの原理と流体の定義が密接に関係しているというのはこういうことである.

厳密な議論はよく分からないというか,自分はそういう証明に興味はないのだが,パスカルの原理と流体の定義は同値だと言ってもいいのではないか？流体の定義が成り立っていればパスカルの原理が成り立つという方向は問題なく言えるだろう.逆はどうなのか？パスカルの原理が成り立っていれば流体の定義が成り立っているとまで言えるだろうか？

しかしこの話は「重力を無視」してしまっている.密閉した容器内であっても,重力があれば深いところほど強い圧力が掛かる.流体内に圧力差が存在しているのだ.それなのに流体は静止した状態で安定しているのはなぜかと聞かれたらどうしようか？

普通に水圧の大きさを求めていたときには流体内に圧力差があることを気にもしていなかったのに,今や,圧力差があるのに流体が動かないでいられる理由をひねり出さなくてはならなくなった！さあ困ったぞ.

パスカルの原理によれば,流体の一部に加わった圧力は全体に同じように伝わるのだった.では,なぜ深いところに生じている強い水圧が浅いところにまで伝わってこないのだろうか？

問題が解決しないうちにさらにもう一つの問題だ.当たり前に思えることほど明確に答えにくい.

さあ,どう答えようか.

なぜ重力と分けて考えるべきなのか

状況を簡単に言ってしまえば,外部から加えられた圧力は密閉した容器内に一定の大きさで伝わるが,それに加えて水圧が普通に掛かることになっている.どちらも同じ「圧力」なのに,重力の影響だけを別扱いして考える必要があるところがどうにも気持ち悪い.

これら二通りの圧力の違いを考えてみよう.外部からの圧力というのは流体を通して伝わってくる.一方,重力による圧力というのは伝わってくるようなものではなく,直接に,地球から流体の各部分へと働きかけてくる.そこを意識すれば疑問は解決できる気がする.

流体内の圧力差によって生じる力は,各部分へと直接に働きかけてくる重力と釣り合うようになっていて,流体は移動しないで済んでいる.

深いところの水圧が伝わってこないのは,それぞれの部分で重力と釣り合っていて,わざわざ他の部分を押してまで力を伝える必要がないから,つまり,それどころではないというか,そのような余力は無いからだ.

別々の疑問に思えていたものは一つのイメージでつながった.

なんだかすぐに納得できなかった例

以前に,水圧というのはその場所よりも上にある水の重みによって生じている,という説明をしたのだった.しかしそれだけだとどうにも納得行かないのが,次の図のような状況である.

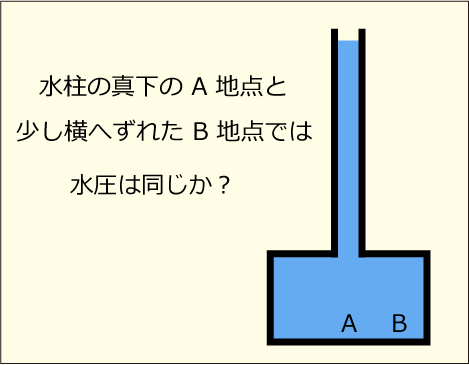
長い水柱の真下ならば上にある水の重みを受けるのも納得が行くが,そうでない横の部分はすぐ上に天井があって,水はそれほど深くはない.それでも分け隔てなく同じくらいの水圧を受けることになるのだろうか？

この水柱がもっとずっと細くて,柱の中の水の量がほんの少ししかないような状況についても思いを巡らせてみて欲しい.そんな少量の水のせいで,容器の下の部分はどこであってもその水柱の高さだけで決まるような強い水圧を受けなければならないのだろうか？

それについてはパスカルの原理を組み合わせることで答えることができる.上の図の状況は,次の図のような状況に等しいと考え直せばいい.

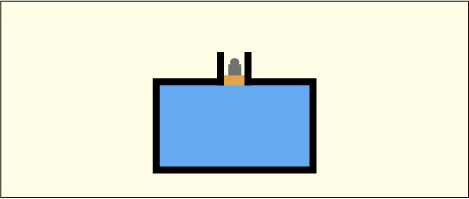
水柱は取り除かれているが,代わりに水柱の中の水と同じだけの重さの重りが乗っていると考えよう.（図では重りが小さすぎて同じ重さに思えないところが申し訳ない.）この重りは外部から加えられた圧力として容器全体に働き,場所に関係なく同じ圧力をもたらすことになる.それに加えて容器内の水には重力に由来する水圧も掛かるわけだから,どこであっても,水柱の一番上から測った深さに対応する水圧を受けると言えるわけである.

なんだか昔すっきりしなかった例

似たようなものだが,もう一つ考えてみよう.次の図のような三角フラスコのような円錐形の容器と円柱型の容器を考え,それらに入った水の水圧を比べてみる.

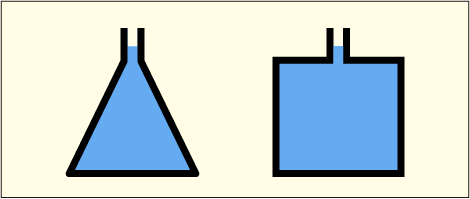
円錐の体積というのは,同じ高さ,同じ底面積の円柱の 1/3 なのだった.水圧というのは,その地点よりも上にある水の重さが原因であると習っている.上の二つの容器に入っている水の量は 3 倍も違うのに,底面付近ではどちらも同じ水圧になるというのがどうにも納得行かないという人も多いだろう.私もそうだったし,同じような意見を聞いたこともある.

これについてもパスカルの原理を援用して説明できる.円錐というのは半径の異なる多数の円柱を積み重ねたものとして近似できる.

これらを次のようにパスカルの原理を適用しながら重ねていけば,先ほどの例と同じことである.

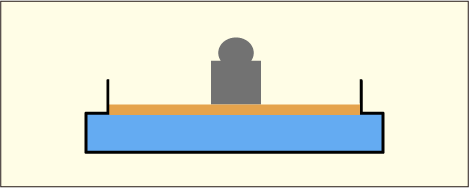
円柱状の容器の一つだけを取り出して、大きな断面積のピストンを取り付けて重りを載せた図

それぞれの層は,一つ上の層の底面の圧力を「外部からの圧力」として受け止め,それが全体に伝わることになる.それに加えて,その層内の水の重みによる水圧が加わって,さらに下の層に圧力を伝えることになる.

このように説明すれば,円柱形ではない容器であっても,同じ深さなら同じ圧力になるということに納得せざるを得ないだろう.理屈の上で納得できても感覚的に納得が行かないとしたら,そこはもう慣れるしかない.

水位が一致しない例

さて,ここまで考えてきた内容から,重要なことが推論できる.容器がどんな形状になっていようとも,流体内の同じ高さでは同じ圧力になるということだ.海の中を水平に泳いでいる限り,ある場所から先では突如水圧が上がるというようなことはない.

例えば潜水中に巨大なオイルタンカーの真下に差し掛かったとしても水圧は変わらない.それについては次回の記事で,浮力と一緒にして検討してみることにする.

では,このことを利用して,次の図のような状況を考えてみよう.

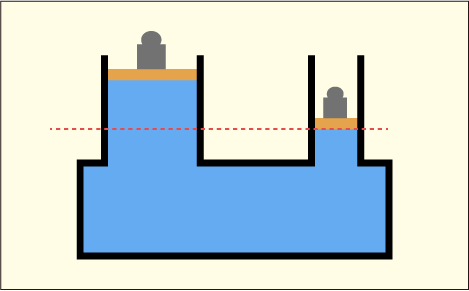
密閉容器に断面積の異なる二つのピストンが取り付けてあり、それぞれの水位が違っている図

このように,二つのシリンダー内の水位に差がある状態で静止しているのを見たとする.「静止した流体中の同じ高さのところでは圧力が一致している」のだったから,図の赤線の高さでの圧力は等しいはずである.赤線よりも高い部分にある水が重りのような役割をして,圧力のバランスを保っているに違いない.

もしも初めに両シリンダーの生み出す圧力が一致していなかったとしたら,すぐに両者の水位が変化して,同じ高さにおける圧力が一致するような状態になったところで安定するはずである.