流体力学：変形速度テンソル

不穏な疑問

前回からの続きである.今後は次のような「ニュートンの粘性法則」が成り立つ流体についてだけ考えることにしようという話になったのだった. この左辺のは接線応力である.前回の例では流体が方向に流れている場合を考えたのだった.

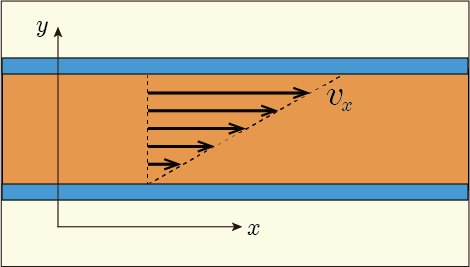
は軸方向を向いた断面に働く軸方向の応力を意味していたのだから,応力テンソルの $T_{yx}$ に相当するだろう.次のように書き直しておこう. 他の面も同じように考えて,応力テンソルを全て埋めることが出来るのではないだろうか？おお,簡単ではないか！なぜわざわざ話を区切ったのか.前回の話でここまで一気にやってしまえば良かったではないか？

ところがこの応力テンソルはどこかおかしい.応力テンソルが対称になっていないと物質内部で勝手に回転が始まってしまって止まらない可能性があるのだった.しかし例えば $T_{xy}$ と $T_{yx}$ を見てみよう.もし対称であるのなら次の関係が成り立っていないといけないはずだ. しかしこれが成り立っている理由がない. v_x と v_y は無関係だからだ.前回の例として使ったクエット流れでも軸方向の流れ v_x があるだけで,それ以外の速度成分は 0 だったのだからこの関係は成り立っていない.

無理やり対称性が成り立つようにしたいのなら次のように置いてみるしかなさそうである. もしこの形が正しいのだとしたら,前回のようなクエット流れの場合にはという形の応力が働いていることになるが,軸方向を向いた面に方向の応力が働いていることになってしまう.

そのような応力が働く理由があるだろうか？

上側の流れが速くて下側が遅いので,間に挟まれた流体は速度差によって転がされるように回転を始めてもおかしくないのかもしれない.そうならないようにぐっと耐えているために応力が発生しているのか,あるいは応力が発生しているから回転しないで持ち堪えているのか,どちらが原因なのかよく分からない.

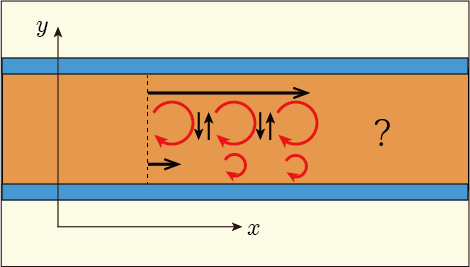
あるいは既に回転をしているのだけれども隣の領域の回転と接することで打ち消し合って軸方向の速度が無いように見えているのかもしれない.すると接線応力はその時に生じる摩擦なのだろうか？いずれにせよ, $T_{xy}$ と $T_{yx}$ の値がちょうどピッタリ同じになる理由がよく分からない.

ヘルムホルツの定理

無理やり対称性が成り立つように小細工をしてみた辺りから既に怪しいのである.もっとちゃんとした理由付けが欲しいところだ.そういうわけで,ちょっと長くなるかもしれない議論に付き合ってもらおう.

前回は方向の流れだけがあって,その流速が座標によって変化する場合を考えたのだった.しかしもっと一般的には座標によっても座標によっても変化している状況も起こり得るであろう.ある地点から微小距離 ( dx, dy, dz) だけ移動した先で流速 v_x がどれだけ変化するかを表そうとすると次のような式になる. v_y や v_z についても同様な式が作れる. これら 3 つの式は行列の形にしてまとめた方が分かりやすい. ここで出てくる 3 行 3 列の行列を「速度勾配テンソル」と呼ぶ.ここではとりあえずという記号で表すことにしよう. このテンソルには,ある点のごく周辺の流れの変化がどうなっているかという情報が入っている.これを対称部分と反対称部分に分けてやると面白いことが分かる.反対称というのは,行と列を入れ替えた時に符号が反転するような性質のことである.どのようにするかというと,このテンソルを半分ずつ二つに分けて,一方には行と列を入れ替えたものを加え,他方からは行と列を入れ替えたものを引くのである.やってみよう. あまりにややこしくなってきたので,第 1 項のテンソルを,第 2 項のテンソルをという記号で表そう. 今後は具体的に全成分を表記するよりも次のように成分表示した方が分かりやすいかもしれない. それぞれの意味を解釈してみよう.まず,の対角成分のみに注目してやると,それぞれ ∂v_x/∂x , ∂v_y/∂y , ∂v_z/∂z であるが,これらは方向に進んだ時に方向の流速が増えていたり,方向に進んだ時に方向の流速が増えていたりする,その度合いを表している.場合によっては減っていることもあるわけだが,増えている場合をイメージして図に表せば次のようになる.

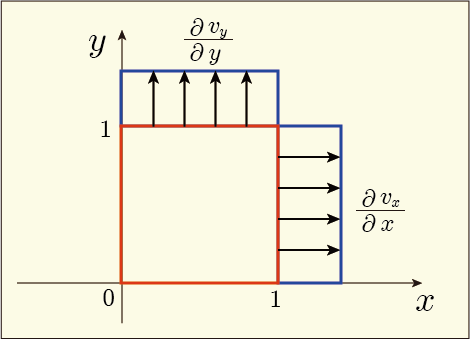
つまり元々立方体だった領域が移動したときに起こる,それぞれの軸方向への伸び縮みを表していると言える.

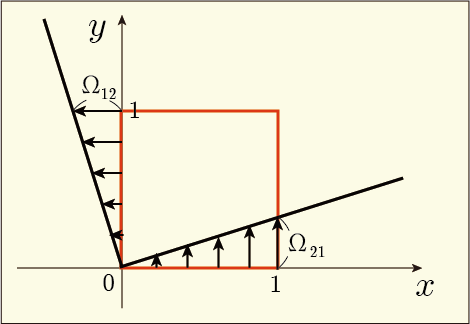
次にの非対角成分について解釈してやろう.図に表すためには平面に関係する部分だけ見てみるといい.それはの左上の 2 × 2 の部分であるが,今は非対角成分についてだけ考えるのだから $E_{12}$ と $E_{21}$ だけに注目するといい.この偏微分の具体的な意味については今は気にしなくていい.とにかく何らかの値が入っており,これらは等しいのだった.だから図示すると次のようになる.

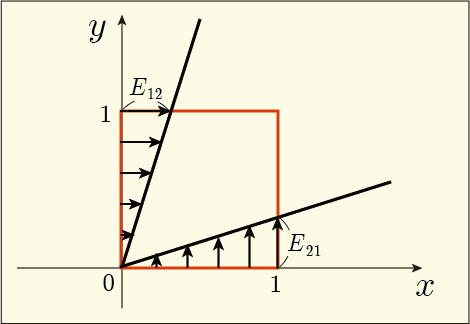
場所を移動するほど移動方向とは垂直な方向に速度が増して、結果として流体の進路が狭くなることを示した図

軸に沿っていた流れは進むに従って軸方向へと逸れていくし,軸に沿っていた流れは軸方向へと逸れていく.つまり,元々立方体だった領域は進路が狭められて行くわけである.ここでは $E_{12}$ と $E_{21}$ が正の値だった場合を図示しているが,負の値だった場合には逆に進路の幅が広がっていく感じだろう.

次にについて考えてみよう.こちらには対角成分は無いから,非対角成分について今やったのと同じように図示してやればいい.成分の具体的な意味は考えなくてもいい.ただとにかく $Ω_{12}=-Ω_{21}$ という関係になっているのだから次のようになる.

場所を移動するほど移動方向とは垂直な方向に速度が増して、結果として流体が全体的に回転することを示した図

軸方向への流れも軸方向への流れも同じ角度だけ同じ方向へとずれていく.つまり,元々立方体だった領域が変形もせずに回転するようなイメージである.

テンソルは流れの伸び縮みやひしゃげ具合を表しており,テンソルは回転度合いを表していることが分かった.それでテンソルを「変形速度テンソル」と呼び,テンソルを「回転速度テンソル」と呼ぶ.

今見たように,どんな流れであってもその微小部分はどこかの方向へ向かって平行移動する動きをしつつ,回転する動きをしつつ,変形しているということである.必ずこのような動きに分解できることを「ヘルムホルツの定理」と呼ぶ.

幾つかの教科書には「変形しないで回転しつつ,同時に変形する動きをしている」という表現が見られるが,このように言われるとまるで異なる現象が同時に起きているようで混乱してしまいそうになる.「平行移動しながら回転する座標系の上で変形する」と言われればもっと分かりやすいと思う.それぞれの座標系の動きの和を取れば,静止系から見た動きが再現されるわけである.

変形具合と応力テンソル

粘性の話に戻ろう.粘性というのは流体の変形具合に関係しているのではないかという疑いを向けてやる.つまり,応力テンソルというのは変形速度テンソルの関数になっているのではないだろうか？いやいや,ちょっと待って！どうして回転速度テンソルの方を無視するのさ？流体の微小領域がそれぞれの点で回転をしていたら,お互いの領域が摩擦を起こして,それが応力発生の原因になっているかもしれないではないか.

それもそうだ.多くの教科書では「変形しないで回転しているだけだから無関係だ」などと言ってその議論が飛ばされる.まぁ,なんとなくそういう気もしてくるわけだが,本当にそう結論していいものかが気になって仕方ない.これについては後で説明した方が分かりやすいのでとりあえず (2) 式の仮定で話を進めよう.

(2) 式の関数の性質を特定するために $E_{ij}$ がごく小さいと仮定してテイラー展開してみよう. 和の記号だらけで複雑そうに見えるが,が 9 個の成分を持つので (2) 式は 9 個の変数 $E_{ij}$ の関数になっており,その一つ一つを偏微分した項の和になっているだけである. $c_{ij}$ は $E_{ij}$ に関係なく定まる何らかの定数である.

さて,ここで強力な制限が課せられる. $T_{ij}$ や $E_{ij}$ については流れ方次第でどんな形もあり得るし,それは現象を観察する人の座標軸の選び方によっても変化するだろう.しかし流体自体には特別な方向がないのだから, $E_{ij}$ から $T_{ij}$ を得る変換の規則についてはどんな座標軸の選び方にも無関係でなくてはならない.どんな向きで流体の動き $E_{ij}$ を見た場合にも,同じ規則でその視点での $T_{ij}$ へと変換されるべきだと言っているのである.

そう考えて眺めてみると,定数 $c_{ij}$ というのは添え字が 2 つある 3 行 3 列のテンソルである.どんな風に座標変換しても同じままであるようなテンソルと言えば,単位行列の定数倍しかあり得ない.つまり,次のように書ける. この $δ_{ij}$ というのは「クロネッカーのデルタ」と呼ばれていて, i=j の時に限って 1 でそれ以外は 0 であることを意味する.

次に (3) 式に出てくる $∂T_{ij}/∂E_{kl}$ という部分に注目してみる.添え字として i,j,k,l の 4 つが使われている.つまり 3 × 3 × 3 × 3 の成分を持つ量であり,こういうのを 4 階のテンソルと呼ぶわけだが,こちらもどんな座標変換をした時にも全く同じままであるという条件を適用してやると次のような形のものしかあり得ない. B,C,D は定数である.どうしてこういう形になるかという議論は省くが,こういう性質を持ったテンソルは「等方性テンソル」と呼ばれているので,詳しく知りたくなった人はこのキーワードで調べてみて欲しい.

(3) 式では 1 次の微小変化までしか書かなかったが,もし $T_{ij}$ と $E_{kl}$ の間に直線的な関係が成り立っていればこれで十分であり,次のような関係になっていると言えるだろう. 話をニュートン流体に限ることにしたのだから, $E_{ij}$ の 2 乗,3 乗の項などは必要なくて,これで十分であろう.

次に,これらの定数の意味を考えていこう.もし流体が静止していれば $E_{ij}=0$ なので, $T_{ij}=Aδ_{ij}$ が成り立つことになる.静止しているときに働く応力といえば圧力しかない.もも応力テンソルの対角成分にだけ存在するものなので,まさに A=-p が成り立つ！……と言いたいところだが,この話はどうもおかしい.

この話は有名な教科書『流体力学（前編）』に載っているもので,座標回転の対称性の議論だけから理論的にピッタリ当てはまる形で圧力が出てくるところが気持ちよくて私も気に入っていたのだが,私は今からこの説明に反旗を翻すことにする.他の教科書といえば,このあたりの説明を避けて天下り的に結論だけを持ってくるものばかりであるから参考にならなかった.

もしそうなら圧力は定数でなければならないことになるし,静止時の圧力は簡単に計算できるのでもはやは未知関数ではないことになってしまう.圧力はそんなにおとなしい性質のものではない.後から粘性のない場合についての具体例を考えてみれば分かるが,圧力は流体の速度と密接に関係していて,粘性の影響がなかったとしても,もっとダイナミックに変化するものである.

応力テンソルが流体の速度の関数だとしたことが間違いだろうか？いや,応力テンソルは確かに流体の運動によって変化するものであろう.しかし,前に導いた流体の運動方程式を見ても分かるように,流体の速度というのは応力テンソル以外の項にも使われている.応力テンソルの値はそれらの項との関係によっても決まるのである.応力テンソル $T_{ij}$ と変形速度テンソル $E_{kl}$ との関係だけで定まると考えてしまったところに誤りがありそうだ.

ではどのように修正すればいいかというと,(2) 式の左辺の $T_{ij}$ は応力テンソルそのものではなく,粘性の存在が応力テンソルに与える影響の追加分を表しているのだと考え直してやればいいだろう.傷は少なくて済むし,多少恣意的に見えてしまう欠点はあるが,間違った論理でもない.粘性が無くても圧力はすでに応力テンソルに入っているので, A=0 だということにすればいい.

先ほどは「反旗を翻す！」などと勇ましいことを言ったわけだが,説明を終えてみるとそれほど大したことを言っているわけではないような気がしてきて拍子抜けだ.書き終わったあとで,同じ著者によって書かれた物理テキストシリーズの『流体力学』に次のような記述を見つけた.「運動しているばあいでも, p に圧力という意味をもたせることにする」これが正確にどういう意味かは分からないが,私が偉そうに説明した内容を一言で表現しているような気もする.しかもこちらの本のほうが先ほどの本よりも以前に書かれているのだ.著者は問題を把握していたにもかかわらず,後に書いた本で表現を修正しなかったのだろうか？よく分からない.

次はである.この項に入っている $Σ_{k}E_{kk}$ が気になるので具体的に計算してやると次のようになる. あれ？なんでこんなところに「湧き出し量」が？非圧縮性流体では div v=0 だったのだから,水や油,あるいは流速が遅いときの空気のような非圧縮性流体を考えるときにはこの項全体を気にしなくていいということになる.しかし後のために残しておこう.

まだ分からないことだらけだが,今のところ応力テンソルは次のような形をしているということになる. 最初に浅知恵で作ってみた (1) 式に近付けようとすれば 1/2 (C+D) を粘性率だと解釈すればいい.(1) 式では対角要素が 0 だったが,この式では予想しなかったものが入っている.前回のようなクエット流れについて計算してみるとこれらの対角要素はたまたま 0 になるので必要性に気付かなかったというわけだ.法則の等方性を考慮すればこの形になるべきだったのである.

これで定数やも片付いたので,定数にも何か名前を付けて別の記号を割り当てよう.まだ意味がはっきり分からないし,流体の変形に関係して出てくるので「第二粘性率」と名付けよう.記号はにしよう. これが今回の結論である.これ以上の変更はないので安心してほしい.あとは残った問題をゆっくり片付けよう.

回転はなぜ無視して良かったか

もしここまでの議論に回転速度テンソル $Ω_{kl}$ も入れて議論していたらどうなっていたかを考えよう. $Ω_{kl}$ の対角要素は 0 なので第 2 粘性率のような項は出てこないだろう. $Ω_{kl}$ は反対称なので,(4) 式と同じところまで進むと次のような関係になるに違いない. なぜ同じ定数が使われるかと言うと,自然界はわざわざ変形速度テンソルと回転速度テンソルとを区別しないで,速度勾配テンソルとしてひとまとめに反応するはずだからである.二つの部分に分けたのは単に人間の理解の都合である.

この C-D が幾つになるのかを考えないといけないのだが,分かりやすい具体例を一つ用意して決定してやれば十分である.流体がどんな状況であっても同じ定数が使われるはずだからである.

そこで変形を起こさず回転する場合というのを考えてみよう.円筒形の容器に水を入れて,容器ごとターンテーブルに乗せて回転させてやると,やがて容器も水も同じように回って,流体どうしの速度差がまるで無い状態が生まれる.まるで静止した流体がそのままの関係を保ったまま回るようなものであり,こういう流れを「剛体渦（ごうたいうず）」とか「強制渦（きょうせいうず）」とか呼ぶ.

この流れの速度場を具体的に書いてやれば反時計回りの場合には v=(-ωy,ωx,0) と書ける.はただの定数だが,たまたま角速度を意味している.これを $E_{ij}$ に代入してみれば期待した通り,至るところで 0 になり,どこにも変形が起きていないことを意味している.そして $Ω_{ij}$ に代入してみれば流体中の至るところで次のような形になる. どの流体要素もその場で同じように自転しているようなものである.ところが今は流体要素どうしに摩擦などが生じるはずもない動きをしているのを我々は知っている.回転するからと言って周りと摩擦を起こすとは限らないわけだ.こうして少し前に気にしていた心配の一つからは開放された.

さて,(6) 式が成り立っていれば (7) 式のような形の接線応力が働いているはずなのだが,そうでもなさそうである.回転の外側に向かって遠心力による擬似的な重力が働いているようなものなので,回転の中心から離れるほどに強い圧力が掛かっているかのようになるだろうが,それは法線応力である.それは圧力の側がそのように変化して実現するであろう.それについては他の機会に計算してみよう.

このようなことを考えていくと C-D=0 と結論して良さそうである.

粘性率は本当は何なのか

$E_{ij}$ というのは対称テンソルであった.対称テンソルは何らかの座標変換を行うことによって必ず対角化できるはずである.その時,新しい座標軸 (x',y',z') 上で次のような形になるであろう. 流体の進路の幅が狭まったり広がったりという色んな変形のイメージを話してきたが,ある方向から見ればそれらは,軸,軸,軸のそれぞれの方向への純粋な伸び縮みだったというわけである.粘性率というのは,そのような形状変化に対する流体内部での抵抗だと見ることが出来るだろう.

二枚の板の間に流体を挟んで滑らせたときに感じる粘り気の強さというのは,このような現象のほんの一面が現れたものだったということだ.あたかも流体の流れの層どうしのこすれ合いのようにとらえてしまって,それだけを頼りにして考えると (1) 式のようになってしまい,本来成り立っている (5) 式を再現することが出来なかったのだった.

誰だ,イメージが大切だなんて言ってたやつは！（前回の記事のタイトルのすぐ下を見よ）

さらに第二粘性率についても意味を考えてみたいが,これ以上話が長くなるのも困るので,次回に引き継ぐことにしよう.