単刀直入に行こう
まずはごく簡単に言い表してみよう.「密閉された容器内の流体の一点に加えた圧力は,流体のすべての部分にそのままの大きさで伝わる」というのが「パスカルの原理」である.
容器が密閉されているのにどうやって圧力を加えるかと言えば,例えば容器の一か所だけ開けて流体が漏れないようにピストンを取り付けて,その上に重りを乗せるのである.ピストンが流体と触れる面積がだとして,重りの質量が
だとすると,圧力は次のように表される.
この圧力
が容器内の流体のすべての場所に加わることになるし,容器の内側の全ての壁もこの圧力
で押されることになる.
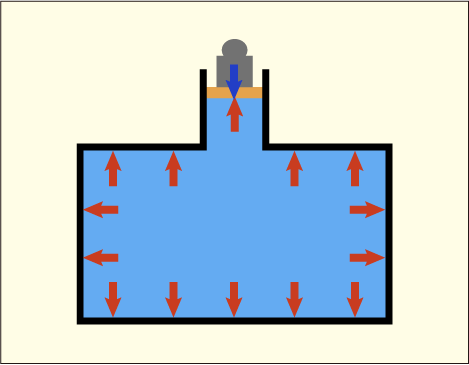
ところが,このような「よく見かける説明」は大変な誤解を生みやすいので注意が必要だ.
問題点は 2 つもある.
大気圧の無視
まず一つの問題は大気圧が完全に無視されているということである.上の図のピストン(板)の部分には実は図に書かれていない大気圧が掛かっており,それに加えて重りによる圧力
が掛かっている.つまり,流体の各部分に伝わる圧力というのは
ではなく,本当は
なのだ.
義務教育では「絶対圧力」ではなく,大気圧を無視した「ゲージ圧力」を使って教えるし,テストでは(特に指定がなければ)ゲージ圧力で答えなくてはならないから,大気圧の存在を気にしてしまうようなちょっと賢い生徒は教えられていることとの矛盾に悩まされるのである.考えすぎは良くないとも言っていられない.たまに大気圧を考慮した発展問題が出題されることもあり,大気圧の存在に気付かされてしまう.そこで考え方の一貫性が保てなくて混乱したりする.
混乱しないためには,世の中には「絶対圧力」と「ゲージ圧力」の二通りの流儀があることと,それらが世の中で使い分けられているという理解は必須であろう.
ダイバーの使う水圧計も,医療で使う血圧計も,工業で使う油圧計も,みんな「ゲージ圧力」を使って表示されているのだから,教育界では実用の方を重視して,みんなで大気圧の存在を無視しているのである.
重力の無視
もう一つの問題点は,容器内の流体自体に掛かる重力が無視されていることである.重りに掛かる重力は考慮しているのに,流体に掛かる重力を考えないのはいかにも扱いが中途半端だ.水圧の存在を説明するときには流体自体に掛かる重力を使って考えていたのに,パスカルの原理の説明ではそれがなくなってしまっているかのような説明は良くない気がする.
実際には,「容器の外から加えられた圧力」と「流体に掛かる重力によって生じる圧力」との合計が存在しており,深さによって圧力が違ってくる.全体に一様に伝わるのは前者の「外部から加えられた圧力」の方だけである.
先ほどの図のような説明では,密閉さえすれば容器内の圧力が一定になると誤解してしまう可能性が出てくる.実際,私がそのような誤解をしていたし,今回の記事のために久しぶりに考え直したとき,本当に合っている考え方はどちらなのかという確信を得るために色々な思考実験をする必要があった.
例えば,海の水を全部覆ったらどうなるだろう?密閉したとたんに深海まで一定の圧力に変わるだろうか?果たして密閉するとはどういうことなのか?重量のある板で完全に塞いでもいいが,その代わりに重さのほとんどない透明ラップでも同じなのではないか?その上から大気が圧力を掛けているのだから,実は透明ラップの存在も必要なくて,大気が海の水を密閉していると考えても同じだろう?そのときに,深海の水圧はほとんど大気圧と同じになったりするだろうか?いや,そんなことはない!
例えば,超科学を持った宇宙人が地球にやってきて,地球人に対して敵対的な侵略活動を始めたとする.彼らは地球をすっぽりと覆って我々から空を奪うような驚くべき構造物を作り始めたとしよう.完全に覆われた瞬間,地球の大気は上空まで圧力一定になって,密度が一定になったりするものだろうか?いや,そんなことはない!
わざわざこのような思考実験をせねばならなかったほどに,私に染み付いた誤解はこれまでしっかり更新される機会がなかったのである.
なぜこのような誤解を生みかねない教え方が続けられているのだろうか?確かに,余計な要素を入れない方が教えやすいというのもある.しかし現実を無視するのは良くない.とは言っても,現実という点について考えると微妙である.よっぽどの専門家でない限りは重力の存在を無視してもあまり問題にならないという「別の現実」があるのだ.
例えば,パスカルの原理を応用した,クレーンやパワーショベルなどの油圧装置の圧力は数十 MPa 程度である.大気圧が 100 kPa であるからその 100 倍程度だろう.しかし装置の落差は 10 m もないくらいであり,10 m に相当する油の圧力は水圧より少し小さいくらいで,1 気圧以下である.つまり,重力は装置内の圧力に数パーセント以下の違いしかもたらさない.
車やバイクにも使われている油圧ブレーキはどうだろうか?伝える圧力はせいぜい数気圧程度である.落差は 1 m もないくらいであるから,大きめに見積もっても 0.1 気圧程度だろうか.装置内を伝わる圧力の 1/10 以下であろう.圧力はブレーキの踏み込み具合,握り具合によって変化するものであるし,重力の影響が少々あったところでほとんど問題ない.しかも一度車体に装着してしまえば高低差が変わったりするようなものではない.装置を固定した状態でブレーキの利き具合を微妙に調整するのだから,高低差などはまったく気にしなくていい.
一方で,高低差を気にしなくてはいけない分野も存在している.血圧というのは 100 mmHg 程度であって,水圧で言えば十数メートル程度に相当する.(だから時代劇なんかで血しぶきが盛大に飛ぶ描写は正しいんだよな.)血圧を測る腕の部分と,圧力源である心臓の高さの落差はほとんどないから,この限りにおいてはやはり重力による圧力差は気にしなくてもいい.血圧を腕で測るのは,もちろん腕が一番測りやすい形をしているというのもあるが,この心臓との高低差がほとんどないという理由もある.腕で測れば,寝ていても座っていても心臓との高低差がほとんど生まれない.状況によっては足首で血圧を測る場合もあるが,その時には姿勢によっては高低差だけで 10 % 程度も血圧が高くなることを考慮する必要がある.
というわけで,今回は私もとりあえず流体に掛かる重力のことを無視して説明を続けることにしよう.確かに,そうした方が楽である.
パスカルの原理の応用
パスカルの原理の応用例は今,上で幾つかの例を出してしまったが,改めて説明しよう.次の図のような状況を考える.
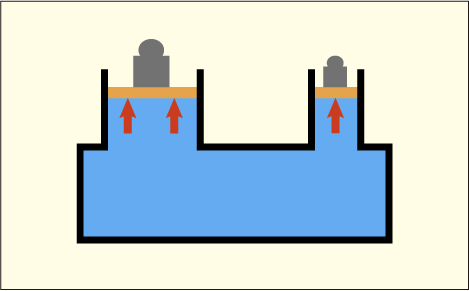
流体を入れた密閉容器に断面積の違う二つのピストンを装備した.断面積の大きな方に重いものを置いても,面積が大きいので,圧力はそれほど大きくならない.一方,断面積の小さな方には軽い力を加えただけでも大きな圧力を掛けることができる.
両方のピストンを押し合った時にどちらが有利だろうか?押し負けた方へと移動することになる.断面積が小さい方が,小さな力で大きな圧力を生み出すことが出来るから,有利になるだろう.
この説明だと,両側からそれぞれ異なる圧力を掛けていて,その結果としてピストンが動くわけである.しかしパスカルの原理というのは厳密には静止した流体で成り立つ話だから,あまり動いてもらっては説明に困る.「静止した流体中の圧力は一定である」あるいは「すぐに一定になるように落ち着く」のであるから,全く同じことだが,両側から押すと考えるより,一方を押した圧力が他方に伝わるというイメージで説明した方がいいのかもしれない.
いかにもパスカルの原理っぽくなるように,説明をやり直そう.流体内では圧力は全体に同じように伝わるので,断面積の小さな方に小さな力を加えるだけで,その圧力がそのまま断面積の大きな方にも伝わるのだった.つまり,小さな力だけで断面積の大きな方の圧力に拮抗して重いものを支えたり,それを少し上回る力を掛けてやればどんどん持ち上げていくことすらできる.断面積の比を大きくしてやればやるほど,小さな力だけで済む.(シンプルでいい説明だ!)
さて,もちろん,一方的に楽ができるわけではない.断面積が小さい方を長い距離押してやっても,断面積の大きな方は少ししか上がって行かない.力の弱い分だけ距離で稼ぐのである.
細いシリンダーから押し出した流体の量と同じ分だけ,太いシリンダー側に入ることになるのだから,ピストンの移動距離は断面積に反比例する.その一方で,力は断面積に比例する.距離と力の積が仕事なのだから,エネルギー保存則を破らない.なぜこんな風に物理法則に都合のいいことがいつもいつもうまく成り立っているのだ?エネルギー保存則を破れなくて大変に悔しい.
とにかく,これを利用すれば,小さな力で重いものを動かすことが出来る!
水門の開閉,跳ね橋の上げ下げ,クレーン,油圧ショベル,油圧ジャッキ,油圧ブレーキなど,色々と応用されている.
流体として水以外のものを使っても原理的には何も変わらない.油を使って応用したものが「油圧装置」である.なぜわざわざ油を使うのかといえば,水と比べて次のような多数の利点があるからである.
・金属に触れても錆びを作らない
・ピストンとシリンダーの間の潤滑油として働く
・粘度が高いので隙間から漏れにくい
・低温で凍らない
・高温で沸騰してシリンダー内に気泡を作ったりしない
・わずかに圧縮性があり,振動を吸収してくれる
・水より軽いので装置全体の重量が軽くできる
どれも,物理学的な理由ではなく,工学的,技術的な理由である.
納得できる重要な性質ばかりであるが,沸騰しないという点についてその重要性を補足説明しておこう.もしシリンダー内に気泡が出来てしまうとどうなるか?気体は圧縮性が高いので,圧力を掛けようとしても,混入した気体の体積だけが弱い力で大きく変化してしまうようになる.ゆるゆるなピストンとシリンダーがもう一つ余計に追加されてしまったのと同じような状況であり,大きく押し込んでも圧力がなかなか上がらなくて力が本来のピストンに伝わらなくなってしまう.わずかな圧縮性は利点に数えられるが,大きく圧縮できてしまうのは困るのだ.
油圧装置の仕組み
油圧ショベルなどを見ていると,シリンダー部分がかなりの長さの伸び縮みをしているのが分かる.油圧ジャッキなどもそうで,車を 1 m か 2 m 近くも持ち上げたりしている.
とは言ったものの,最近では油圧シリンダーだけで大きく動かそうとする設計のものはかなり減ってきている.機械式のてこの原理と組み合わせることで長い距離を動かしている.油圧シリンダーは小型化されて目立たないところに隠されていたりする.せっかく油圧で強い力を生み出したのに,てこの原理で力を弱めてしまうなんていうのは本末転倒な使い方ではないかと思うのだが,適材適所,工学とはそういうものだ.つまり,油圧装置自体が小型化した上に大きな力に耐えられるようにもなったので,力の増幅装置というよりも動力の伝達装置としての使い方がメインになってきているのである.
強い力を出すための代償として,反対側では長い距離を動かさないといけないのだと説明したのだった.すると,目に見えないところには細くて長い長いシリンダーが仕込まれてあって,その長さは数十メートルほどもあるのだろうか?とてもそうは見えない.途中で折り曲げられていたらピストンがうまく通れないではないか.ひょっとしてぐるぐると巻かれた形の長いパイプの中をピストンがかなり素早く移動していたりするのだろうか?
上の図のような説明ではそのような想像をしてしまったりするのだが,現実の装置の発明者たちはもっと賢い.
わざわざ細いシリンダーにピストンを押し込む動作をさせる必要はない.油だけを相手のシリンダーの中にチューチューと押し込んでいってやればいいのだ.そのためにはポンプを使う.流し込むための管が細ければ細いほど,いや,正しく言えば管自体の太さは関係なくて,ポンプの部分の断面積が小さいほど,小さな力でどんどん油を流し込めることになる.
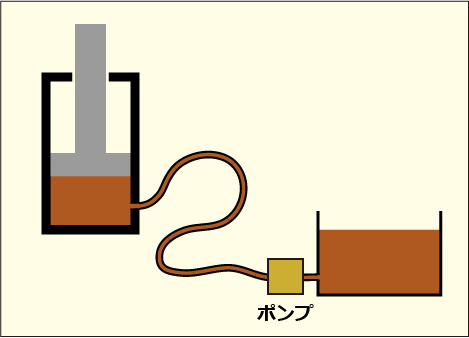
図の右側にあるのは流し込むための油を入れてある容器であって,そちらに圧力は掛かっていない.比較的小さな力のモーターで高速に大量の油を入れたり戻したりしているのである.
ではそのポンプはどのような仕組みなのだろうか?船のスクリューのようなものを回してもいいのだろうが,動いている間は何とかなるにしても,止めた途端に隙間から逆流してきてしまうだろう.油に圧力を掛けて一方方向に流し込めて,しかも逆流を起こさない仕組みのポンプが要る.それについて気になった方は「油圧ポンプ」で検索してみてほしい.賢い仕組みのものが色々と存在している.とりあえず Wikipedia の「油圧ポンプ」の項目がおすすめである.
タイヤ交換などに使う手動の油圧ジャッキというものも安く売られていたりするが,あれは持ち手を漕ぐことによって灯油のポンプと同じような仕組みで油を一方へ押し流していて,圧力弁で逆流を防いでいるのである.

Amazonで油圧ジャッキを見てみる?
ポンプを動かす方法が手動というだけであって,原理はほぼ同じである.
油圧ブレーキの仕組み
上の話だけでは大掛かりな感じがするので,もう少し単純な仕組みの応用例も説明しておこう.車やバイクなどの油圧ブレーキである.近頃は自転車にも使われたりする.
ブレーキというのは,回転しているディスクやドラム型の物体を強い力で挟み込むことで摩擦を発生させて,その回転を止めてやるという仕組みである.ブレーキを掛けない状態ではギリギリ触れるか触れないくらいの距離で待機していて,そこから 0.1 ミリかそこら動かせば十分である.
実際のところ,普段から少しくらい触れていても問題ないくらいである.力が掛かっていなければ摩耗したり異音が発生することもほとんどないので当たるに任せていたりする.
パスカルの原理の説明図にあるような巨大な水槽も要らない.その部分は本質ではないので細いパイプに代えてしまっても構わない.断面積の違う二つのシリンダーを直結してやってもいいくらいである.途中はくねくねしていても構わない.次の図のような感じである.
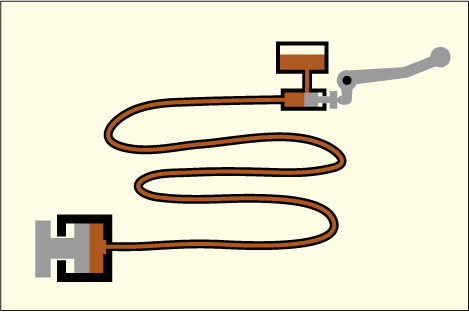
油がピストンの隙間から漏れて徐々に失われる可能性があるので予備タンクを付けてあるのが普通だが,そこにはピストンを押し込んだ時には圧力は掛からないようになっており,原理として重要な部分ではない.(しかし装置を正常に保つという,安全のためには重要である.)
バイクや自転車では,ブレーキレバーを 2~3 センチ程度握ることで,てこの原理でレバーの根もとが油圧の細い方のピストンを 4~5 ミリ程度押し込んで,反対側では 1 ミリもないくらいの僅かな距離だけ動くといった感じである.実際にはアソビがあるので,そっくりそのままその比率で力が増幅されるわけでもなく,ある程度握ってからやっと力が掛かり始めるとかいう感じである.
図では省略してあるがあちこちに簡単なばねが仕込んであって,手を離せばピストンが元に戻るようにもしてある.
機械式のブレーキだと,パイプの中に金属ワイヤーを通して,それを引っ張ることで動力を伝達しているが,力の増幅は行われないし,あまり複雑な経路を通そうとするとパイプとワイヤーの摩擦も増えてくる.一方,油圧方式は力の増幅もできるし,パイプさえ通れば力はスムーズに伝達される.多少高価であるという弱点があったのだが,あまり気にならないほどになってきたので,自転車でもよく見かけるようになってきた.
このように,油圧は力の増幅装置であるだけでなく,力の伝達装置としても使われるのである.
次回予告
まだ多少,書き足りないことがあるのだが,応用の話で横道に逸れて長くなってしまったので今回はこれくらいにしておこう.重力とパスカルの原理との関連をもう少し議論しておきたいのである.










