インピーダンスの意味
次はコイルやコンデンサーや抵抗を「組み合わせた」回路について考えてみよう.
コイルやコンデンサーを通った電流は,位相が進んだり遅れたりするのだった.しかしそれは電流が個々の部品を通過するたびにずれていって,どんどんとずれ方が蓄積されて大きくなるというわけではない.回路のどの場所を見てもつじつまが合うような電流が,回路全体でしっかり調整された形で流れるのである.
例えば,複雑な回路であったとしても,「ある一つのコイルを流れる電流」と「そのコイルの両端の電圧」を見れば,前回話したような関係は依然として成り立っている.また,コンデンサについても同じことが言える.
抵抗もそうだ.抵抗の場合は電流と電圧にずれは生じないのだった.だから,抵抗を流れる電流とその両端の電圧だけを見れば,それは普通にオームの法則が成り立つ形になっている.
もう少し詳しく話そう.抵抗とコイルとコンデンサーを直列にして交流を流した場合,この 3 つの部品にはどれも同じ大きさの電流が同じタイミングで流れる.一本の線なのだから当然である.それぞれの電流に位相のずれはない.
ところがそれぞれの部品の両端の電圧はそれぞれがずれている.抵抗の両端の電圧には電流との位相のずれはないし,コンデンサーの両端の電圧は電流より 1/4 周期だけ遅れているし,コイルの両端の電圧は電流より 1/4 周期だけ進んでいる.
さて,この回路全体の電圧を知りたければ,この 3 つの部品の両端の電圧を全て足し合わせることになるわけだが,その結果はどんなものであろうか?
数学に詳しい人なら,これはひどく複雑な波形になるわけではないことを知っているだろう.足し合わせる波形の周波数がどれも同じである限り,周波数がもとと変わらない単純なサイン波になる.ただし,位相は足し合わせる前の電圧のどれともずれた形になっている.このことを単純に示す公式は高校で習う数学の範囲には見当たらないが,ちょっと手間を惜しまなければ説明は可能である.3 つの波の足し算は面倒だから,とりあえず,2 つの,振幅と位相の異なる波の足し算をやってみよう.
二つの波はそれぞれ,三角関数の合成の公式を逆に使って次のように分解して表記できる.
これらの和を取ってから,今度は三角関数の合成の公式を普通に使えば次のような変形ができる.
この
の部分を
に置き換えて考えれば,今回の話と同じだ.周波数が同じで位相や振幅の異なる波を幾つ足し合わせても,位相が変わるだけで,周波数や波形は変わらないということが分かるだろう.
位相がどれくらい変わるかというと,足し合わせる個々の波形のうち,振幅の大きかった方の位相により近くなるのである.
もう一つの例を話しておこう.今度はそれぞれの部品を並列にした場合で,どの部品にも同じ交流電圧が掛かる.しかしそれぞれに流れる電流は違っていて,振幅も位相も異なるのである.ただ,周波数だけはどれも同じだ.この回路全体に流れ込む電流はどうなっているかというと,3 つそれぞれの電流を足せばいいのである.
これも,先ほど説明したばかりの理屈によって,周波数が元と同じで,位相がずれただけの交流電流が導かれてくることが分かる.
このような具合であるから,抵抗やコイルやコンデンサーを複雑に組み合わせたものを一つの集まりとして外から見ると,「そこを流れた全電流」と「その全体に掛かっている電圧」は 1/4 周期だけどちらかへずれるのではなく,単純には計算出来ないようなずれ方をするのである.もちろん,先ほどのように三角関数の合成の公式を駆使すれば,どれだけずれるかはちゃんと計算できるはずである.
そのときの電流と電圧の最大値も計算できるので,それらの比を考えれば,ここでも抵抗に似た概念が導き出せるだろう.これを「インピーダンス」と呼ぶ.
インピーダンスとは,抵抗(レジスタンス)やリアクタンスを合成したものであり,交流の流れにくさを表す概念だと言えるだろう.この単位もやはり Ω(オーム)である.
複素数の助けを借りる
先ほど,インピーダンスを計算するには,三角関数の合成の公式を駆使して,ややこしい計算をする必要があるような説明をした.しかし,複素数の助けを借りることで,もっと少ない手間で,そして,図形的イメージで,インピーダンスの大きさどころか,位相のずれの具合まで簡単に計算できてしまうのである.
そのためには複素数について少々学ぶ必要があるが,習うより慣れろ,というやつで,その意味をあまり理解していなくても計算だけは一定の手続きで出来てしまう.微分や複素数を知らない小学生でも覚えることができる.その方法だけ教えてほしいという人もいるだろうが,ちゃんと理解できていれば感動して楽しくなれるので,なんとか説明してみよう.
しかしここで複素数について一から話し始めるわけにも行かないので,付いてこれなくなった人は「複素関数論」を学んでみてほしい.最初の 3 つほどの記事を読むだけで十分であるが,必要以上のことにまで触れているので,そちらを読む方が難しいかも知れない.
まず,次のような「オイラーの公式」というものが前提である.
は虚数単位であり,2 乗して -1 になるような数である.数学では
を使うが,電子工学では
は電流を意味することが多いので,虚数に
を使うのが普通なのである.
今までは交流電圧や交流電流を表すのに主に関数を使って来たわけだが,これは別に
関数を使っても構わなかったのである.単なる好みの問題であった.例えば電流を
と表してもいいわけである.ところが,今,ちょっと思い切って,電流を
と表してみることにしよう.ちょっとこれは思い切りが良すぎる気がする.先ほどのオイラーの公式によれば,これは,
と書いているに等しいわけで,第 1 項の実数部分は確かに (2) 式に等しいけれども,第 2 項の虚数部分は全く余計であって,付けておく意味が分からないからである.実はこの虚数部分は全く気にしなくて構わないのである.(3) 式のように表現することで,微分計算が楽に済むという利点を拝借したいだけであり,実数部分にのみ着目していれば問題ない.
本題に入る前に,まずその辺りをもう少し説明しておこう.(3) 式を時間で微分したらどうなるだろうか.
指数関数の微分というのはとても簡単で,もとの関数部分は変化せず,その肩に乗っている部分を微分して掛ければいいだけである.確認のため,この結果をオイラーの公式を使って三角関数を使った形に戻してみよう.
第 1 項が虚数になり,第 2 項が実数になった.実数の方だけを見ていれば,(2) 式を微分したのと結果が変わらないのである.虚数部分は完全に無視して構わない.
ところで先ほどから,という形ばかりが出てきて,非常にごちゃごちゃしてしまっている.交流の話では
というのはいつもひとまとまりで出てくるので,式を簡略化するために,次のような記号を導入しよう.
この
のことを「角周波数」と呼ぶ.物理では「角振動数」と呼ぶが,電子工学の話をしているのでその流儀で行こう.三角関数の位相は
で一周して元に戻るので,
というのは 1 秒間に位相がどれだけ進むかを表したものだと考えればいい.わざわざ無理してイメージを描かなくても,単なる
の略記号だと思っておいても本当に問題ない.
これを使うと今まで書いたものは本当にすっきりする.電流は
と表してもいいし,
と表してもいい.この微分は
と表してもいい.微分するという作業が,単に,
を掛けるという作業に置き換わっているのである.
抵抗とコイルの直列
試しに,抵抗とコイル
を直列につないだものを考えてみよう.直列で一本の線なのだから,どちらに流れる電流も同じである.この時,両方の電圧の合計を計算してみよう.キルヒホッフの法則(一周すると電圧は 0 になること)より,
が成り立っており,移項すると
である.ここで,電流を (4) 式で表すことにすると,
のような関係になっていることが分かる.交流電圧
と交流電流
とを比べてみれば,
の部分が抵抗に相当する量を表している.これをインピーダンスと呼ぶのであった.しかしここには虚数
が含まれており,実数ではない.これは複素数だ.それでこれを「複素インピーダンス」と呼ぶのである.複素インピーダンスは
という記号で表し,単位はやはり Ω(オーム)である.
この意味を解釈してやらなければならない.この複素数
は,複素平面上に表せば,次のようである.
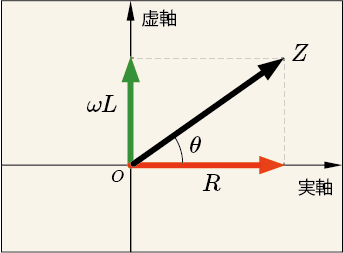
抵抗と,コイルのリアクタンス
が作る合成ベクトルのような位置にある.
ところで,複素数どうしの掛け算をするときにはとても簡単な図形的ルールが成り立っている.まず,それぞれの複素数を複素平面上に表して,それぞれに原点から矢印を引き,その矢印の長さと,実軸(横軸)からの角度を求める.その矢印の長さを「絶対値」と呼び,その角度のことを「偏角」と呼ぶ.そして,それぞれの絶対値どうしを掛けあわせ,それぞれの偏角どうしを足し合わせる.そうして得られた絶対値の積と,偏角の和が,それぞれ,結果の複素数の絶対値と偏角を意味している.このようにして結果の値が複素平面上のどこにあるかが図形的に分かるのである.
つまり,今回の場合,
であり,
と
という二つの複素数を掛け合わせて複素数で表された電圧
を求めているのだから,電流の最大振幅
にこの
の矢印の長さを掛けたものが電圧の振幅になり,この
の矢印が向いている角度
分だけ電流の位相を進ませたものが,電圧の位相になるということだ.
コイルのみの場合には電圧の位相は電流より 1/4 周期進むのだが,抵抗が存在しているせいで,全体としてはそれほどは進んでいないように見えるのである.
抵抗とコンデンサの直列
では抵抗とコンデンサの直列を考えてみよう.先ほどのようにやると少し面倒なので,コンデンサの両端の電圧と電流の関係を先に求めておこう.コンデンサはの関係になっており,この両辺を時間で微分することで,
が得られるのだった.ここでコンデンサーの両端の電圧を
だと仮定すると,
という関係が得られる.これを変形すれば,
という関係であることが言える.
ここからがやっと本題だ.抵抗とコンデンサを直列にした時の合計の電圧は,
であって,このたびの複素インピーダンスは次のように表せる.
だから次のように書いてもいい.
これを複素平面上に図示すると,次のようになる.
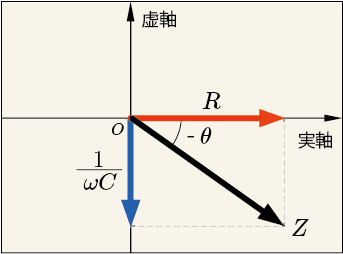
コンデンサのリアクタンスは虚数軸の負の方向のベクトルで表され,それと抵抗
が作る合成ベクトルのような位置に
がある.
RLC直列インピーダンス
では,抵抗とコイルとコンデンサを直列にすると,全体のインピーダンスはどうなるだろうか.
いちいち式を作らなくても今までのパターンから分かるだろう.
である.コイルとコンデンサのリアクタンスが虚軸の上で互いに打ち消す形になっており,勝ち残った成分と抵抗とを合成する形になる.そんな風に考えなくても,全部の成分を複素平面上でベクトルのように足し合わせればいいわけだ.
図形的に明らかだが,わざわざ式で表したければ,の絶対値は,
であるし,電流に対して電圧がどれだけずれるかについては,
という形になっている.
直列インピーダンス
ここまでの話でパターンがつかめたと思うが,抵抗のみ,コイルのみ,コンデンサのみのインピーダンスはそれぞれ,
であると考えればいい.そしてそれらが直列になっている限りは,これらの和を作ればいいのである.複数のインピーダンスが直列になっている時,全体のインピーダンスは,
のようにして計算できる.
並列インピーダンス
交流電圧と交流電流と複素インピーダンスの関係がという関係で結ばれているのだから,これはパターンとしては普通の抵抗についてあれこれ計算したのと変わらないのである.複数の複素インピーダンスが並列に繋がれている場合には,全体のインピーダンスは,
のようにして計算できる.
抵抗とコイルの並列
並列にした場合のインピーダンスが複素平面上ではどんなイメージになるかについても知りたいと思うことだろう.しかしそれは複雑すぎてあまり助けにはならない.
一目見てみれば納得すると思うので,試しに抵抗とコイルの並列インピーダンスについて計算してみよう.
これで簡単にイメージできるものではないことが分かってもらえただろう.










