空孔理論
原子構造の解明や中性子の発見の歴史の流れに従って話しているうちに,1950 年代くらいの内容まで入ってきてしまった.しかし少し時代を遡って別の流れについても話しておかないといけない.
1928 年,ディラックが相対論的な量子力学を考え,「反粒子」なるものが存在するだろうと予言した.彼は,何もないように見える真空にも実は無数の電子が詰まっていて,そこから飛び出した電子が通常の粒子として観測され,それが抜けた穴が反粒子として観測されるのだというイメージの理論を発表したのである.
この理論は後には場の量子論によって再解釈されることになるのだが,今回の話ではまだそこまで踏み込む必要もないので,この古いイメージのままで説明しよう.
この理論によると,真空に対してある程度のエネルギーを与えれば,電子とその反粒子が対になって飛び出してくるだろうということになる.これが「対生成」である.そして粒子と反粒子が再び出会えば,その両方の質量分のエネルギーを放り出して消滅し,もとの真空に戻る.これが「対消滅」である.
反粒子というのは存在の欠けた穴なのだから,電場を掛ければ電子とは逆の方向に動く.まるでプラスの電荷を持っているかのように振舞うだろうというわけだ.詳しくは量子力学のページの「ディラックの海」という記事でも説明しているので参考にしてほしい.
対生成の条件
対生成を起こさせるために,真空に対してどうやってエネルギーを与えたらいいかが問題だ.高エネルギーのガンマ線を撃ち込むにしても,一体どこの何を狙って撃ったらいいだろう.
実のところ,真空中をどれだけ高いエネルギーの光を走らせようとも対生成は勝手に起こったりはしないのである.もしそんなことが起これば運動量保存則とエネルギー保存則を満たさなくなるからだ.重要なことだからちょっと計算で示してみよう.
エネルギーのガンマ線が,質量
の粒子と反粒子に変化して飛び去る状況を考えてみる.このとき,運動量保存則を満たすためには,ガンマ線の進行方向に対して対称な角度で飛び去らないといけない.次の図のような感じだ.
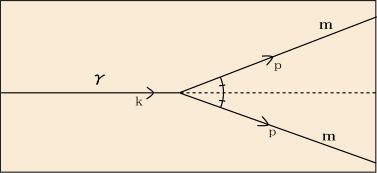
要修正:この説明には間違いがあります.運動量保存を満たすためには粒子と反粒子が上下に同じ角度で飛び去らなくてはならないと書いていますが,上下方向の運動量成分が同じ大きさを持っていれば良いので異なる角度で飛び去る可能性を考えなくてはなりません.計算はもう少し大変になりますが,やはりそのような状況も禁止されていることが導けます.角度を使わずに運動量の横向き,縦向き成分を使って計算したほうが楽なのではないかと思います.
飛び去る粒子と反粒子の運動量の大きさをそれぞれだとする.ガンマ線の運動量を
で表そう.まず運動量保存則により,
が成り立つ.そして相対論的なエネルギー保存則により,
も成り立たなくてはならない.さて,
と
の関係は
であるから,これを使って (1) 式と (2) 式をつないでやれば,
となって,左辺は常に負であり右辺は常に正となる.つまり両辺は 0 だとでも考えない限り矛盾する,というわけだ.
まぁ,なぜ二つの保存則がそんなにまでして守られなければならないのか,という疑問は生じるだろうが,それはもう少し深いところの理論まで降りて行って,対生成を記述する根本の法則が時空の対称性に縛られていることを見ないといけない.保存則というのは時空の対称性と関係しているのだった.
対生成の条件 2
エネルギーが十分であっても単独のガンマ線では対生成を起こすことはできないことが分かった.ではどうすれば良いかというと,運動量の過不足を引き受けてくれる別の粒子の助けがあればいいのである.
静止している質量の粒子にエネルギー
のガンマ線をぶつけることを考えよう.衝突前のこの系の全エネルギーは
であり,全運動量は
である.そして衝突後もこれらの量はそのまま保存するはずだ.
衝突後には質量の粒子と反粒子が新しく生まれたとしよう.これら二つの粒子と,標的となった質量
の粒子はそれぞれ色んな方向へ飛び散るだろう.しかしそういう状況を考えると非常に複雑で手に負えなくなるので,飛び散らずに済むようなギリギリ最低のエネルギーについて考えることにする.つまり,3 つの粒子は互いに離れることなく同じ速度で移動してゆくのだとする.元のガンマ線が持っていた運動量を保存する形で仲良くかたまって運動しているわけだ.,実際はこんな状況ではすぐにまた一緒になって対消滅が起きてしまうのだが,計算のための都合良い仮定なのだから深くは考えないことにする.これら 3 つの粒子が静止して見えるような座標系に乗り換えて考えると,この状況の相対論的な全エネルギーは
であり,全運動量は 0 である.
こうして全エネルギーや全運動量の値が二通り出てきたことになるわけだが,どちらも同じ状況についての値である.ただし,観察している座標系が違っている.座標系が違えばエネルギーや運動量は異なる値を示すのは当たり前で,これらを直接比較するわけにはいかない.しかしここで相対論の知識が役に立つのである.という量は不変量であったことを思い出そう.
というのは,全エネルギーを
で割ったものだった.これに当てはめてやれば,次の等式が出来上がる.
この条件に当てはまる最低エネルギー
は幾つになるだろう.
さて,ガンマ線を当てやすい相手と言えば,原子核だ.原子番号の大きな核ほどでっかくて当たりやすい.電子の質量
に比べて原子核の質量
は遥かに大きいので,
となる.つまり,電子 2 個分の質量に相当するエネルギー以上のガンマ線を原子核に当てれば,対生成が起こりうるのである.余ったエネルギーは粒子の運動エネルギーに転化されることになる.
原子核だけでなく,ガンマ線が電子に衝突して対生成が起こることがある.この場合はなので,
となる.この場合にはガンマ線が粒子の質量エネルギーよりもかなり大きなエネルギーを持っていないと対生成が起こらないのである.
対生成の条件 3
ガンマ線を何らかの物質粒子にあてる以外にも対生成を起こす手段はある.それはガンマ線どうしを正面衝突させるという方法である.
一方から来るエネルギーのガンマ線に,もう一方から同じエネルギーのガンマ線を衝突させることを考える.このときの全運動量は 0 である.この結果として,静止した粒子と反粒子のペアが生まれれば,それはエネルギー保存も運動量保存も満たされていることになるだろう.もっとエネルギーが高ければ,粒子のペアは運動エネルギーを得るだろう.その時にそれらの粒子が互いに正反対の方向へ飛び去るのであれば全体の運動量は 0 であり,保存している.理論上はこういう事もありうる訳だ.
もちろん,この衝突の様子を別の慣性系から眺めれば違って見える.互いにエネルギーの異なるガンマ線が衝突した結果,ペアの粒子が生じるのを見ることになるだろう.そういうパターンも許されているわけだ.
このような現象があるというのは単なる推論ではなくて,もっとちゃんとした理論から導かれることである.なかなか難しい技術だが,こういう「光子光子衝突」実験も行われていて,ある程度の結果がでているようである.
対消滅の条件
対消滅については,割と簡単に起きる.要するに,粒子と反粒子が出会えばそれでいいのである.
ただし,エネルギー保存則と運動量保存則を満たすためには,結果として二つのガンマ線が発生し,それらは互いに反対方向に飛び去る必要があるだろう.まぁ,必ず正反対だとは限らない.重心系で観察していればそうならないといけないだろうが,それ以外の系(二つの粒子の速度が異なるように見える慣性系)で観察していれば,ガンマ線が飛び去る方向は正反対からは少しずれて見えるに違いない.
いやいや実は,対消滅の時に出てくるガンマ線はいつも二つきりだとは限らないのである.それ以上発生する事もありえて,それでも保存則を満たすことができる.三方向に 120°対称に飛び去ってもいいだろうし,他のパターンもありうる.三つでも四つでも幾つでもいいはずだ.
幾つのガンマ線が飛び出してくるかはどういう条件で決まるのだろうか.それは確率で決まり,二つ出てくる確率が最も高いのだそうだ.そういう確率を計算するにはどういうことを考えたらいいのだろう?まだよく分からないが,まぁ,いつかその辺りの理論までたどり着けることを期待しよう.
ガンマ線が一つきりしか飛び出してこないことだってあり得る.しかしそのためには運動量の過不足を引き受けてくれる別の粒子との反応が必要になるのだが.
対消滅については他にも疑問がある.二つの粒子が空間の一点で出会うのはなかなか難しいだろうと思う.粒子の直径が小さければ小さいほどだ.現代の理論では電子は大きさの無い点だと考えられると聞いたことがある.しかしそんなものどうしが衝突など出来るだろうか.量子力学以前の考え方をするならば,無限に小さな点どうしはどんなに近くを通っても互いにすれ違うだけだろう.それとも電荷で引きあうのだろうか?先ほどは粒子と反粒子が出会えばいいと軽く書いたが,どれくらい近づけば対消滅が起こるのだろう.
少し前の「ラザフォード散乱」の記事で書いたが,粒子どうしが反応を起こす確率は断面積の概念を使って表すことができるのだった.対消滅を起こしたり,別の粒子に変化したりする衝突確率も同様に断面積の概念で表せて,これを「崩壊断面積」と呼ぶのである.いずれはこの値を計算する理論のところまでたどり着きたいものである.
陽電子の発見
1932 年,「陽電子(ポジトロン)」が発見される.電子と全く同じ質量で,電荷だけがプラスなのだった.それでポジティブな電荷を持つエレクトロンという意味で名付けられた.
対生成や対消滅も確認されたことから,これぞまさしくディラックが予言していた「電子の反粒子」であることがはっきりしたのであった.
霧箱
この頃の新粒子の発見には,霧箱という,人工的に一瞬だけ霧を発生させられる装置を使っていた.正確には霧ができるギリギリ直前の状態を手動のポンプを操作することによって一瞬だけ作り出すのである.その状態になった容器の中を高エネルギーの粒子が通過すると,白くて細い糸のような軌跡が見られるのである.
なぜ軌跡が出来るかと言えば,高速の粒子の影響によって電離した空気の分子が核になって,雲を生じるからである.飛行機雲と似たような原理だ.飛行機雲は飛行機が進むにつれてゆっくりと伸びてゆくが,粒子の軌跡の場合は突如一瞬にして線が現れる.だから良く観察して考えてみないことには粒子がどちらからどちらへ向かって進んだ跡なのかの判断さえ難しい.しかしゆっくり考えている間もなく消えるのである.
これがけっこう綺麗なものなので,みんなにも見せてあげたいと思った.良い動画はないかと少しの間探してみたのだがどうも見つからない.いや霧箱の実験の動画自体は沢山あるのだ.しかしそれらは最近になって一般向けの手軽な実験として工夫されるようになった方式の霧箱の画像なのである.それらの方式では容器の中が対流しているので,軌跡がすぐに渦を巻きながら煙のように広がってしまう.出来たばかりの軌跡はかなり繊細な線なのでカメラには写りにくいのだろう.やはり肉眼で見ないとその本当の美しさが分かってもらえないかもしれない.
宇宙空間ではかなり強いエネルギーを持った放射線が飛び交っている.これらを「宇宙線」と呼ぶ.地球の磁場や大気の層がそれらを防御してくれているので地上にはあまり届かないが,空気の薄い高い山などに登れば,かなりの量が観測できる.霧箱を利用した観測装置をそういう場所へ持って行って,何か変わった性質を持った粒子がないかどうかを根気よく探すのである.
このような調子で,やがて色々な粒子が宇宙線の中に見つかるようになる.そして電子以外の粒子にも反粒子があることがはっきりしてくるのである.










