複素数とは何か
2 次方程式を解こうとすると虚数を含む解が出てくることがあるのだった.虚数というのは 2 乗すると負の値になるような不思議な数である.
虚数を含む解は二つの実数
と
を使って次のように表される.
は虚数(imaginary number)の頭文字に由来しており,2 乗すると -1 になる数値を表している.工学系では電流を表すのに
をよく使うので,虚数
の代わりに
を使うこともある.
を「実部」と呼び,
を「虚部」と呼ぶ.このような数値
は
と
という複数の成分を持つという意味で「複素数」と呼ばれる.複数の成分を持ってはいても,これで一つの数値なのである.実部を含まない場合,つまり
かつ
の場合の
を「純虚数」と呼ぶ.
の実部 (Real Part) を表すときには
という表現を使うことがある.
の虚部 (Imaginary Part) を表すときには
という表現を使うことがある.
「虚数」という名前からは,
が「現実には存在しない数」「偽の数」「架空の数」というイメージが付きまとう.しかし勉強を進めるにつれて,虚数とは「ある種の論理を構成するためには必要不可欠の数」「存在して然るべき数」だと分かるようになるだろう.虚数を認めて使いこなすようになる前の人類の論理は狭いものだったのである.
基本ルール
これから複素数どうしの間の基本的な計算,つまり加減乗除の方法を説明しよう.そのために,の他に
という数値を用意する.まずは足し算から.それぞれの実部どうし,虚部どうしを足し合わせればいい.
引き算は書く必要もないだろう.
や
が負の数だと考えればいいだけだし.
掛け算はであることさえ考えれば,普通に展開して計算できる.
難しいところなしだ.こんなものを公式として暗記するやつの気が知れん.おっと,失礼.
残るは割り算だが,どう考えたらいいのかとちょっと首をひねることになるかも知れない.しかし一度知ってしまえば簡単だ.分子と分母に同じ数を掛けても良いということを利用して,分母を実数にしてしまえばいい.
これもわざわざ公式のように覚えるようなものではない.考え方さえ頭の隅にあれば,必要なときにすぐに計算できるだろう.
複素平面
このように複数の成分を持つ数というのは,もはや数直線の上に並べて視覚的に理解することができない.そこで,軸を増やして平面の上に表そうということになった.横軸で実部を表し,縦軸で虚部を表すことにする.横軸を「実軸」と呼び,縦軸を「虚軸」と呼ぶ.
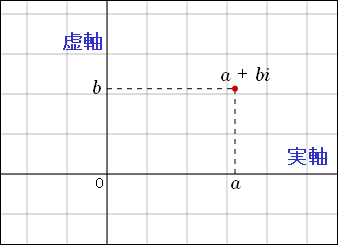
複素数とは平面上の点で表される数値なのである.このような平面を「複素平面」あるいは「ガウス平面」と呼ぶ.
このように表すことで複素数の振る舞いが非常に分かり易くなるのである.スムーズな理解のために,まずは幾つかの用語を定義することから始めよう.
複素数値を平面上の点として表すと言ったが,点の位置を指定するためにちょっと変わった方法を使うこともできる.複素平面の原点から複素数を表す点まで矢印を引いて,ベクトルのように表してみる.
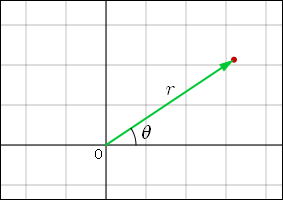
この時,この矢印の長さをとし,この矢印の実軸からの角度を
で表す.反時計回りの角度がプラスであり,時計回りをマイナスとする.
と
を指定することで,ただ一つの複素数値を決定することができる.まさに極座標のようなものだ.複素数
は次のように表す事ができるだろう.
のことを複素数
の「絶対値」と呼び,
のように表すこともある.絶対値というのは実数のときにも原点からの距離を表していた.同じ考えを複素数にまで拡張したのである.
だとすると
は次のように計算できるだろう.
また,
のことを複素数
の「偏角」と呼び,時には
と表すこともある.
積の図形的意味
二つの複素数値と
を絶対値と偏角を使って表してみる.
そしてこれらの積を計算してみよう.
とてもシンプルな結果だ.ちゃんと実部に
関数が,虚部に
関数が来ていて,掛ける前のそれぞれの複素数値と同じ形式になっている.これがどういうことかというと,積の結果の複素数値を複素平面上に表してやると,その絶対値は二つの複素数値の絶対値の積になっており,その偏角は二つの複素数値の偏角の和になっている,ということだ.積の計算結果が図形的に非常にイメージしやすいものになっている!
要するに,複素数を掛けるというのは,元の数値にその絶対値を掛け,その偏角の分だけ元の数値を複素平面上で回転させるという意味を持つ.
例えば虚数を掛けるというのは,複素平面上にある数値を 90°だけ回転させるという意味を持つし,さらに
を掛ければ -1 ,すなわちこれは 180°回転させるという意味になる.さらに
を掛ければ
,すなわち 270°の回転.そしてもう一度
を掛ければ 1 に戻る.これは 360°回転して元に戻るということだ.
マイナスとマイナスを掛けるとプラスになるのが理解できない,と言っている人に時々出会うことがあるが,私の経験上,このイメージを利用して説明してやると納得してくれる率が高い.こんな具合に話す.「マイナスを掛けるというのは,数直線上で方向をひっくり返すという意味なんだ.だからマイナスにもう一回マイナスを掛けるとプラスに戻るってわけさ」
複素数を平面上に表すというアイデアは人為的な小細工かも知れない.しかし複素数の積が持っているこの性質は,この表示上の工夫をするか否かに関係なく元から備わっていたものである.複素平面での表示は,それなしには見えにくかった性質を人間に分かりやすい形で示してくれているのである.
複素共役
最後にもう一つ,紹介しておこう.複素数の虚部の符号だけを変えたものを
の「複素共役」と呼び,物理学者の多くは
という記号で表す.一方,数学者は上にバーを付けた
という記号を使うことの方が多い.ここでは物理のための数学を説明しているので物理流のやり方で行こう.
こんなどうってことないものにわざわざ名前を付けて記号まで用意してやるのはなぜかというと,色々と便利な使い道があるからである.どのように便利なのかを今のうちから一言で説明することは難しい.とにかく,複素数を応用的に使うようになると色んな場面で出てくることになるだろう.
ここでは便利さの一例だけを紹介しておこう.複素数とその複素共役
を足し合わせると何になるか?答えは
だ.だから複素数
の実部だけを取り出して計算に使いたい時,次の右辺のような表現が使われることがある.
あるいは複雑な式変形をした末にこの式の右辺のような形が出てきた場合,「なぁんだ,それが意味するのは
の実部のことじゃないか!」と分かって,途端にイメージしやすくなったりするわけだ.
同じように,虚部だけを取り出したい時には次の右辺のようにするといい.
他にも次のような関係も成り立っている.
複素共役との積を計算すると,絶対値の 2 乗になるというわけだ.さっきの「積の図形的意味」をあてはめて考えればそれほど不思議なことでもないだろう.
こういうことを説明しているうちに,これくらいは知っておいた方がいいかな,という関係が他にも幾つかあるのを思い出した.
今こんなものを並べて示されても,必要性が感じられないので退屈かも知れない.しかし勉強を続けていれば近いうちに必ず使うときが来るから,暇なときにでも自力で確認しておいてほしい.いや,これくらいは今すぐにでも確認できるはずだ.何となく覚えておいて,その時が来たら思い出してくれればいいだろう.










