物理数学：一致の定理

紹介

今回はちょっと脇道にそれて,複素平面上でテイラー展開できることの効能について話しておきたい.「一致の定理」と呼ばれるちょっと驚くような定理があって,その証明にテイラー展開が活躍するのである.

一致の定理とは,ある領域で正則な,一見したところ異なるように見える二つの関数があって,その領域内のほんの短い線上で二つの関数が一致することが確かめられたなら,その領域の全体で二つの関数は一致することが言えるというものである.

これを聞いて誰もが驚くべきなのかどうかは私には分からない.「ふーん」と思うだけでも構わないような気もする.正直なところ,すごいことのような気もするし,当たり前のことのような気もする.「たまたまほんの一ヶ所で一致してる部分があったからと言って,全体が等しくなってるなんて,複素平面上の関数というのはいかに正則性に縛られていることか！」と驚くのが正解なのだろう.しかし「一ヶ所といえども同じ振る舞いをするなら同じ関数以外ありえないんじゃない？」という感覚もある.

使ってみれば凄さが分かるということもある.とにかく証明してみよう.

証明

まずは,「短い線上で一致する」というときの短い線がどんなものかを定義する.それは複素平面上の異なる 2 点とを結ぶもので,途中の経路が z(t) で表されているとする.また,後の都合のために, z'(t)≠0 としておこう.これはを時間にたとえるならば,一時的にでも途中で止まることがないようなイメージである.二つの点は離れてさえいればどんなに近くても構わない.

二つの関数がこの線上で常に等しいというのだから,それは次のように表される. 両辺を微分するととなるが, z'(t)≠0 としておいたので, が言える.同じように繰り返せば,何度微分しても等しいことが言える. もちろん,これは始点においても言えることだから, が成り立っている.

今は二つの関数が正則であるような領域内で考えているが,始点からある程度離れたところには正則でない領域が存在することもあるだろう.正則でない領域までの最短距離を半径とする円を考えれば,その円内では二つの関数は正則であり,「始点を中心とする」テイラー展開ができるはずである. ここに (1) 式を使えば, f(z)=g(z) であることが結論できる.最初に仮定したのは「短い線上で二つの関数が一致する」ことだったが,今は「始点を中心とする,正則でない領域までの最短距離を半径とする円内で,二つの関数が一致する」と言えるまでになったのである.

さて,これから,このようなことが言える範囲を正則な領域全体に広げたい.その為にはどうしたらいいだろうか？テイラー展開は正則でない点に阻まれてしまうので,自由に範囲を広げるわけには行かないのである.

正則な領域内の任意の点をとしよう.そして先ほどの始点からまでを結ぶ道を引いてやる.この道は正則な領域を通ることにしておこう.

先ほどは始点を中心とした,ある半径までの円内で二つの関数が一致するという結論を得た.この半径より少し内側で考えるのが望ましいから・・・,例えばを中心とする半径 r/2 の円を考え,その円と「からまでを結ぶ道」の交点をとしよう.このを新しい始点にして,先ほどと全く同じ議論が進められるに違いない.

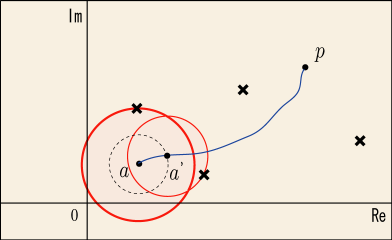
これでもう分かるだろうか？こうして範囲を広げながら,目標とする点を範囲に含められるように徐々に近付いてゆくのである.

念のため,もう一周くらい同じ話を繰り返しておこう.我々は先ほどまでと同じ理屈によって,「始点を中心とする,正則でない領域までの最短距離を半径とする円内で,二つの関数が一致する」と言えるようになるだろう.この円の半径は「最寄りの正則でない領域までの距離」になっていて,先ほどとは違う値だろうからとしよう.この新しい円より少し内側で考えたいから,を中心とする半径 r'/2 の円なんてものを考え,その円と「からまでを結ぶ道」との交点を a'' とする.この a'' を新しい始点にして,先ほどと全く同じ議論を進めるのである.

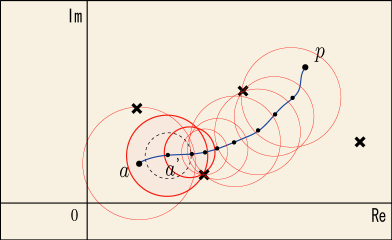
内部が正則であるような円を付け足しながら証明範囲を広げていくことを最後まで続けた図

こんな具合にして,正則な領域内のどこであっても,正則でない点を避けながら,テイラー展開によって徐々に範囲を広げてゆくことができる.点はどこに選んでもいいから,「正則な領域の全体で二つの関数は一致する」ことが結論できるのである.

加法定理

ついにこの時が来た.複素関数論の最初の方で,「三角関数の加法定理などが複素平面上でも成り立っていることを後で簡単に示すことができるようになる」という話をしていたのを覚えているだろうか？それを今からやってみよう.

加法定理の一つとして次の式を例にしよう. この式は,が実数の時には成り立っているのだった.実軸というのは複素平面の一部であり,そこで左辺と右辺の関数が一致していることが言えているのだから,一致の定理を使えば複素平面上でも成り立っていると言えるだろうという理屈だ.しかし丁寧に説明しようとすれば 2 段階を経なければならない.

まず二つの複素関数 f(z) と g(z) を次のように置くことにしよう. は実数の定数であるが,は複素数の範囲で変化するものとする.この二つの関数は実軸上では一致することがすでに知られており,それぞれは複素平面の全域で正則であるから,一致の定理により,次の式が複素平面の全域で成り立っていることが言える. この式は任意の実数について成り立っている.

では次の段階へ進もう.今度はを複素数の定数であるとして,二つの関数を次のように置く. が実軸上にある時にはこの二つの関数は一致することが (2) 式によって分かっているから,一致の定理によって,が複素平面のどこにあっても次の式が成り立つことが言える. このようにして加法定理が複素平面の全域で使えることが言えるのである.実数で成り立つ他の色んな公式についても同様にすれば良い.

解析接続

一致の定理から得られるイメージを支えにして,新しい考えが導入される.

まず複素平面上の限られた領域のみで定義された関数 f(z) というものを考える.この限られた領域の外ではこの関数の値は定義されていない.そのようなことが起きるのは,大抵 f(z) がテイラー展開のような無限級数で表されておリ,ある範囲外では値が収束しないからである.

この f(z) の他にもう一つ別の関数を考え,それを g(z) としよう.この関数も定義域が制限されているが, f(z) の定義域と g(z) の定義域とに重なる部分があったとする.

ここでちょっと変わったことになっていて,その重なった定義域内では二つの関数が全く同じように振る舞うのを見たとする.つまり,それぞれの関数の見た目は全く違うにもかかわらず,与えられた変数に対しては全く同じ値を返すということである.

これをどう解釈したら良いだろうか？一致の定理によって,定義域が共通している部分のごく一部であっても二つの関数が一致しているなら,その共通部分の隅々まで二つの関数は一致すると言えるのだった.一方の関数にとっては,共通の定義域とそうでない部分とで別の関数を使っているわけではないし,それはもう一方の関数にとっても同じだ.共通の定義域とそうでない部分とを区別しているわけではなく,同一のルールに従って値を出している.ならばこれら二つの関数は,それぞれの定義域を足し合わせた広い範囲内においても同一の関数だとみなしてしまって良いのではないだろうか？

このように,見た目の異なる関数を,同一の関数の別の領域における異なる表現だとみなすことにして,定義域を繋いで広げてゆくことが出来る.これを「解析接続」と呼ぶ.

関数の解析性,つまり微分できるという性質のことだが,それを根拠にして定義域を繋いで行くのでそう呼ばれているのである.

解析接続の例

今説明したイメージ通りの単純な実例を紹介するのはなかなか難しい.

正則な関数をテイラー展開で表してみても収束半径は無限大になるので,それ以外の別の形の関数を導入して定義域を広げて行こうとすることに意味も面白味もない.だから例としては不適だ.それなら,正則でない点を幾つか含むような関数をテイラー展開したものを例にすれば良いだろうか？いやいや,それでさえも本末転倒だ.なぜなら,テイラー展開する前の関数の形は,すでに複素平面上の広い範囲で定義されている形だろうからだ.我々は「狭い範囲でしか定義されていない関数を仕方なく他の形で表す」ような例が欲しいのだ.そして,その「他の形で表された関数」も定義域が制限されていた方が面白い.もし一方の定義域が他方の定義域を包み込むようなものなら,定義域の広い方を使えばいいのだから,「二つの異なる関数を同一の関数と見做して定義域を広げよう」というイメージではなくなってしまう.

そこで茶番劇を演じることにしよう.幾つかの点は見て見ないフリをして欲しいのだ.まず,次のような級数で表された関数を持ってくる. この級数の収束半径は 1 であることが収束半径の判定法の計算で導かれる.つまりこれは |z|<1 の範囲でのみ意味を持つ関数である.

次に別の関数を見てみよう. これは 1+i を中心にして展開されていて収束半径が 1 であり,定義域が一部重なっている.そして,その重なった部分では f(z) と g(z) とは全く同じ振る舞いを見せるのだ.

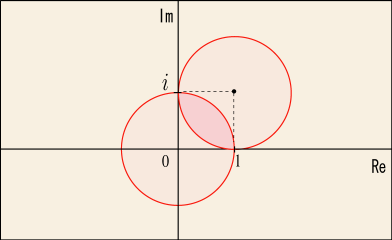
というわけで,この二つを同一の関数と見なして,両者の定義域を合わせた範囲をこの関数の新たな定義域だと考えることにするのである.

ここまでの話のどこが茶番劇かというのを話しておこう.(3) 式は初項 1,公比の等比数列の無限級数であって, |z|<1 という条件の下で次のような関数に等しいという公式が良く知られている. 実は g(z) というのはこの関数をテイラー展開して作っただけのものである.だから定義域が重なる部分で同じ変数に対して同じ値を返すのは当然だったわけだ.このような種明かしの部分は解析接続とは関係ないことなので,楽屋裏の話ということにしておいてほしい.(4) 式のような広い範囲で値を返すすっきりした形の表現がバックに存在していることは必要ではないのだ.

さて,こんな調子で定義域を広げていくと,例えば z=2 を含むような範囲でも定義できる関数をテイラー展開で作れて,それは z=2 に対してを返すだろう.それを f(z) とを同一の関数だと見なすからと言って, などという「いたずら」を仕掛けて読者を不思議がらせようという人もいる.「正の整数ばかりで和をとったものが負の値に等しいとは！？」しかしこういうものは正しい表現とは言えない.(3) 式はあくまでも |z|<1 の条件下でしか使えないものだからだ.

対数関数の解析接続

解析接続を使うことで,二つ前の回の最後の方で話した対数関数の無限多価性を別の角度から説明することも出来る.

log_e z は z=0 が正則でないから,どの点を中心にしてテイラー展開しても収束円はそこに引っ掛かる.色んな点を中心にしたテイラー展開を考え,定義域が重なるところを利用して次々と繋いで行き,原点の周りをぐるっと 1 周してくると,なんと,元の関数とは繋がらずに, 2πi だけズレるというのである.まるで無限の螺旋階段を回るようなイメージになっているのだ.

これだけ聞いても何のことか分からないだろうから具体的な説明をしてみようと思ったのだが,実際に試してみると話がかなり長くなってしまった.予定外だが仕方ない.とりあえずここで区切って,次回はそれだけを説明することにしよう.