スピン状態の全体を把握したい
スピンの状態は次のようにスピン上向きとスピン下向きの状態の和として表せるのだった.
と
はどちらも複素数で,次のような規格化条件を満たしている.
しかしこれだけでは全体像がどうにも把握しづらい.複素数はそれぞれ実数 2 つ分の自由度を持つので合計 4 つの自由度があり,それが規格化条件で制限されているので 3 つの自由度が残っていることになる.スピン状態は一体どんな範囲を動き得て,どれが現実のどんな状態に対応するのだろう?それはまるで 3 次元内を移動するようなものだろうというのは分かるのだが,どんな形になっているのだろうか.いや,どんな形にたとえて表せば人間にとって分かりやすいだろう?
上に書いた式ではと
が複素数として変化する範囲が分かりにくいので,記号の使い方をご破算して次のように表現し直してみよう.
こうすれば
,
,
,
は実数だということになるし,規格化条件は
と表しておけばいい.
さらに単純化を進めたい.全体の位相を変化させたものは物理的意味が変わらないのだったから,その部分を別にしてしまおう.
これで物理的に肝心な部分は括弧の中だけだということになる.
の部分はひとまとめにして独立した一つのパラメータとして扱ってもいい.次のように記号の置き換えを行って表現をすっきりさせてみよう.
ここで
,
と置けば,規格化条件はいつでも自動的に満たされるようになるのではなかろうか.
物理的に区別できる状態は括弧の中の
と
の二つの角変数だけで表されることになる.自由度は 2 次元に減った.これらの角変数を緯度と経度というイメージで図示すれば,あたかも地球儀の表面のそれぞれの点がそれぞれに違った物理的状態を表すかのように対応させられそうだ.面白くなってきた.しかしどちらの変数を緯度と経度に割り当てようか.それに,変域はどう考えたら良いだろう?
も
も
の範囲で変化してもいい.しかし球面の一点が物理的な状態に一対一に対応するという点では問題がある.例えば
なら状態は
だが,
では
となる.マイナスが付いているが,これらは位相が異なるだけであり,物理的状態は同じであるとみなされる.そう考えると
は
の範囲で変化すれば十分だということになる.一方,
の動く範囲は
で問題ないだろう.
こうなると少し問題が出てくる.経度の方にはを当てはめて
の範囲で動かそう.問題は緯度の方だ.赤道上を緯度 0°とする地球儀とは違って,
が北極になるようにするにしても,
の範囲だけでは球面を埋め尽くすことが出来ない.
なら状態は
だから,
の値が変わっても位相が変わるだけであり,赤道上の全ての点が物理的には同じ状態を意味することになるだろう.出来るならこの状態は南極点の一点に対応させたい.
そこでもう一度,使う記号を考え直そう.申し訳ないが再びご破算だ.次のような図を考えて,図の方のや
を基準にする.
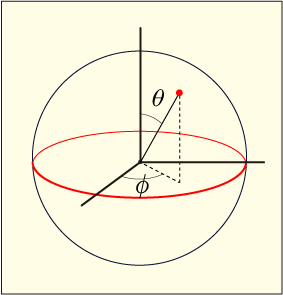
この図に従って式の方を調節することにしよう.は前と同じまま使えばいい.
はこの図では
の範囲で動き,
なら北極,
なら南極である.それで,式の方を次のようにしてやれば良さそうだ.
これなら
や
の引数が
の範囲に収まるだろう.
この図とこの式を採用すれば,全ての状態が重なりなく球面上の点で表され,北極がに相当し,南極が
に相当することになる.この図の球のことを「ブロッホ球」と呼ぶ.
位相の違いはこの図の上には表されていないが,もし必要なら位相の違いを表す薄膜が球面全体にあるようなイメージを持っていれば良いだろう.
と思ったが,これはちょっとまずいのである.図の北極と南極のところでは位相が異なるにもかかわらず,物理的には同じ意味を持つ状態だというので一点に無理やり繋げてしまっている.それで「位相までを含めたありとあらゆる状態」を考えてしまうと,実は互いの状態はこのようなイメージでは繋がっていないのである.気になる人はSU(2)の構造について書いた物理数学の記事を参考にして欲しい.
他の状態はどこにある?
ここまではと
の組み合わせで考えてみたが,他の軸についてはどうだろう?例えば x 軸の上向きの状態というのは次のように表せるのだった.
あらゆる状態を球面上に表現したはずだから,この状態もブロッホ球面上のどこかの点に対応しているはずだ.これは
かつ
の場合に相当する.地球儀で言えば赤道上に位置する.
他の状態も調べてみよう.
これは
かつ
であり,先ほどの
のちょうど裏側に位置する.
y 軸についてはどうか.
これらも
で表現できそうだ.つまり赤道上にある.
については
と
であり,やはり互いに球の反対側である.
図で表すと次のようになっている.
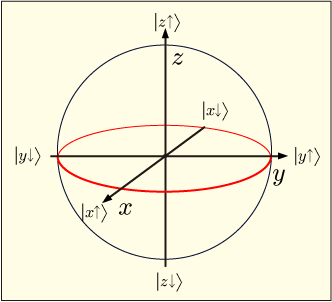
スピンというのは複素数で表された神秘的な量というイメージだったが,直交座標の中に置かれたごく普通の球面上の一点を指す矢印だというイメージになってしまった.
注意
「z軸方向のスピン上向きが確定した状態」はブロッホ球面上では原点から真上の方を向いているが,それと同じ状態は物理的には次の図のようなイメージに近いのであった.
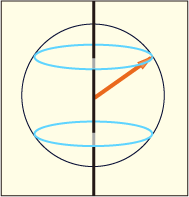
スピンが真上を向いているわけではないのである.
ブロッホ球は,スピンが取り得る状態の範囲を視覚的に分かりやすく表現し直しただけのことである.これは現実をそのまま表したものではない.さらにブロッホ球による表現では全体の位相の自由度も省略されているのだった.
それでも「分かりやすいことは正義」なのである.










