スピンのラーモア歳差運動

歳差運動の復習

回転するコマは重力によって引き倒されそうになってもそれとは垂直な方向に力が働いて,軸の先端が水平面をぐるぐると回るような動きをする.これを「歳差運動」と呼ぶのだった.

円運動をする電荷にも同様な現象が起きる.円運動する電荷は磁気モーメントという概念で表されている.よく知らない人はこちらの記事を先に勉強してきてほしい.磁気モーメントというのは,微小な電磁石のようなものであり,一様な静磁場を掛けた時に磁力によって引き倒されそうになるのだが,コマと同じ原理によって傾けようとする方向とは垂直な方向に力が働くことになり,磁気モーメントベクトルの先頭は磁場の方向に垂直な面内をぐるぐると回り始めることになる.これを「ラーモア歳差運動」と呼ぶ.

さらには原子の周囲を回る電子の磁気モーメントでも似たような事が起こる.電子の軌道角運動量 l=nℏ と磁気モーメントの間には理想的には次のような関係が成り立っている. この $μ_{B}$ はボーア磁子である.もしを整数で表しておけばこの分母のは必要ないのだが,ここでは入れておくことにした.電子のスピン s=±ℏ/2 の場合にはなぜかこの式をそのまま使い回すことができず,さらに 2 倍する必要がある. なぜ 2 倍する必要があるのかについてはちゃんと理由があって,別の記事で説明してある.

今回の話ではスピンが作る磁気モーメントがラーモア歳差運動を起こす様子だけに集中して説明するつもりである.

スピンというのは本当によく分からない.軸に沿って測ってやると上向きか下向きの二つの状態しかないのだが,それでいて軸方向の成分や軸方向の成分が 0 だというわけでもない.不確定性原理によって同時には値を確定できないだけなのである.つまり,軸成分がもし +ℏ/2 だったとしても磁気モーメントベクトルが軸に沿って真上を向いているわけではない.ベクトルの方向が確定しているわけではないのである.そんなぼんやりした存在に対してラーモア歳差運動の古典的イメージを当てはめて想像することは無理に近い.

しかし量子力学的な計算を使って似たような振る舞いが導けてしまうのである.

z軸に磁場を掛ける

量子的な状態の時間変化についてはシュレーディンガー方程式を使えばいいのだった. この式に,スピンまで考慮した状態を次のように表して代入する. 今はスピン状態の時間変化だけに注目したいので空間的な分布である φ(x) については定常状態だとしてある.ハミルトニアン $\hat{H}$ も空間分布には無関係なものを使うつもりである.すると代入した時に φ(x) の部分は全く無視されるので両辺から消してしまっても構わない.結果として次のような方程式を考えればいい. ハミルトニアン $\hat{H}$ については,スピンの固有状態に作用させた時にエネルギーが取り出せるような行列を考えればいい.磁気モーメントに静磁場を掛けたときのエネルギーは内積で表せるので,例えば磁場の向きを軸の正の方向に選べば,磁気モーメントの成分の値との積を使って表せる. スピンが上向きの時にエネルギーは正で,下向きの時に負になる.スピン上向きと下向きをそれぞれのように表すとすれば,ハミルトニアンは次のようなものを使えば良い. こうすればちゃんと $\hat{H}ψ=Eψ$ が成り立っている.解くべき方程式は次のようになるだろう. 成分ごとに分けて書けばもっと単純である. この形の微分方程式は定番のものであり,すぐに解けて,解は次のようになる. ここで導入されたやはスピンの初期値によって決まる任意定数である.また角振動数はであり,古典力学で「ラーモア角振動数」と呼ばれているものと全く同じものである.

古典力学にはなどというものはほとんど出てこないので,これが含まれる式を古典的なものと全く同じものだと言われてもすぐに信じてもらえないかもしれない.ラーモア角振動数というのは古典的には磁気回転比と磁場の積である.一方,ボーア磁子 μ_B というのは電子の磁気回転比にを掛けて作ったものなので,結局この式ではは打ち消されてしまって,内容的に全く同じだと言えるのである.

ここではいかにも物理らしいこだわりで「ラーモア角振動数」と書いているが,あまり一般的に通用する言い方ではない.応用的分野では「ラーモア周波数」と呼ばれることのほうがはるかに多い.角振動数だろうが,それをで割った振動数だろうがあまり区別なくどちらもそう呼ばれる.

そもそも物理学が理論的にラーモア周波数に向き合う機会はあまりなくて,ほとんどは NMR(核磁気共鳴)装置や医療系のMRI(磁気共鳴画像診断)装置の原理の説明で使うことがほとんどである.工学系の勢力が強いのである.

さて,今導いた結果を |z↑>} や |z↓>} に当てはめてみても,あまり面白い結果にはならない. C=1, C'=0 や C=0, C'=1 になるだけである.つまり,もし最初に |z↑>} だったなら,位相が変化するだけであり,ずっと |z↑>} のまま.最初に |z↓>} だったならずっと |z↓>} のままである.

ではもう少し面白いことが起きることを期待して,スピン上向きと下向きの重ね合わせ状態である次のような状態から始めたらどうだろう？これまた,スピン行列のそれぞれの位相が変化するだけであり,重ね合わせの割合が変化するといったような面白いことは何も起きない.しかしそれぞれの成分の位相の変化の正負が違っているので,時々刻々と位相差に変化が起きているようだ.分かりやすいように表現し直してみよう. スピン行列の上側の成分を基準にして見てやるような式変形をしてみたのである.こうすると,下側の成分との位相差がラーモア周波数の 2 倍の速さで変化しているのが分かる.さらに書き方を変えると,これはこういうことである. これは前回の記事でやったブロッホ球の理論に合わせた形式である.この 45°というのはブロッホ球の上で考えると, $θ=90^{\circ}$ の位置に相当し,ちょうど赤道上を角速度で回転していることになるのである.

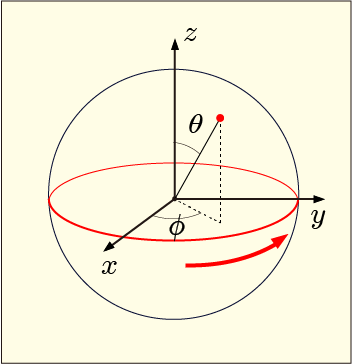
ここから考えを広げていって他の初期状態を考えてみても状況は同じようなものである.初期位置がブロッホ球上のどこにあっても回転の角速度は変わらない.ブロッホ球の軸を中心にして一定の角速度で回転を始めることが分かる.

先ほどは「何ら面白いことは起きない」というようなことを言ったが,それは軸に沿って測定した場合のことしか考えていなかったからで,実はすごいことが起きている.先ほど考えた初期状態というのは,軸に沿って測定した時に上向きとなるような状態だったのである. ところが軸方向に磁場を掛けてしばらく待つとという状態に変化しているというのである.軸に沿って上向きだった状態が,徐々に下向きとして観測される可能性が増え始め,ついには逆転するようなことになるというわけである.

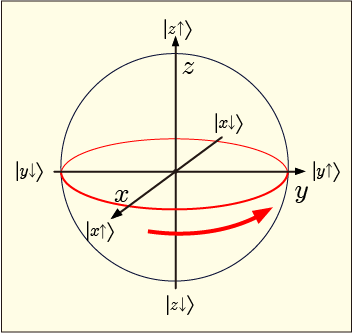
ラーモア歳差運動によってx軸上向き状態が下向き状態へと変化することをブロッホ球を使って表した図

どの座標も対等なので,きっと軸や軸の向きに磁場を掛けた場合には,軸方向のスピン成分の重ね合わせの割合が変化するようなことが起きるのだろう.軸の向きで磁場を掛ければ,ブロッホ球上のあらゆる初期状態が軸を中心に回転をするのだろうし,軸でも同様のことが起きるに違いない.

x軸に磁場を掛ける

ここで話を終えてもいいくらいだが,気になるのでちゃんと計算で確かめてみよう.

軸の正の向きに静磁場を掛けるとする.その時のハミルトニアンはどう表したらいいのだろうか？それほど難しくはない. |x↑>} や |x↓>} に働きかけた時にエネルギーが $±μ_{B}B_x$ として出てくるようなものを考えればいい. このパターンはパウリ行列と同じ構造である.それにさえ気付けばあとは前と似たようなことをするだけなので途中を軽く省くが,つまり次のような方程式を作って解けばいい. 成分ごとに分けて書けば次のようになる. これは二つの式に二つの関数が入り混じって存在しているが,解くのは難しくない.一番単純な解き方としては,最初の式を b(t)=… という形に変形して 2 番目の式に代入するというものだろう.結果は次のようになる. 任意定数とは a(t) と b(t) とで共通のものを使わねばならず,2 つの式は独立していない.の定義は先ほどと変わらないと言ってもいいくらいだが,細かいことを言えば先ほどは B_z だったものが今回は B_x に変わっているのでもう一度ここに書き直しておこう. この結果がどんな振る舞いをするのかを調べてみたい.例えば t=0 において |z↑>} となる条件で任意定数を決めてやると, となるので, C=1/2 かつ C'=1/2 である.つまり,次のようになる. これは予想通り,ブロッホ球の上での軸を中心にした回転である.動きが分かりやすいようにブロッホ球の理論の形式に書き換えると次のようになる. ブロッホ球上での緯度と比べれば θ/2=ωt という関係になっているから,やはりブロッホ球上を θ=2ωt という角速度で回転する事が分かる.

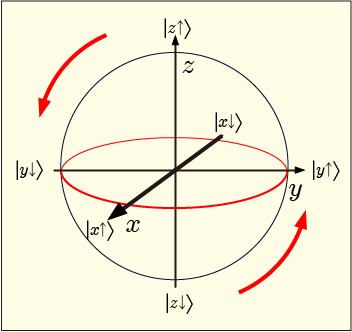
x軸に磁場を掛けたときにはブロッホ球の上での状態の回転が別の軸に沿って起こることを表す図

元々 |z↑>} だった状態が,徐々に重ね合わせの割合が変わって行き,しばらく待つと完全に |z↓>} になってしまうのである.更に同じだけ待てばまた元の状態に戻ってくるし,戻したくなければ途中で磁場を切ってやればいい.

これはすごいことだ.何か代償があるのではなかろうかと疑いたくなるが,エネルギーの消費などは起きていそうにない.今は磁場は軸方向に掛かっているのであって,スピンはその方向に対しては少しも変化していないからだ.

任意の状態が軸を中心にして回転しているかどうかを確かめてみたいが,これは簡単ではないので諦めよう.ブロッホ球の緯線や経線の方向に沿わない動きをするので分かりやすい式にはなりそうにない.最初にやった軸方向に磁場を掛けたときの状況からの類推で満足しよう.

y軸に磁場を掛けるのはもうやらない

軸に沿って磁場を掛けた場合については似たようなものなのでもうやめておこう.もしやろうと思ったらハミルトニアンはスピン行列の成分の形を使えばいいはずだ. ところで,磁場の方向を座標軸に合わせないで任意の方向に掛けた場合にはどうなるだろうか？磁場をそれぞれの座標成分に分けてやって,今まで使ってきたものを合計すれば合計のエネルギーが求まるはずなのだから,次のようなハミルトニアンを使えばいいはずである. ここで試すことはしないが,もし必要となれば理論的にはこのように計算することが可能だろう.