量子力学は間違っている?
アインシュタインは量子力学に反対した.しかし決して邪魔したわけではない.彼は人一倍考えていた.
真剣になって考え,反対してくれる人がいるのは心強いものだ.誰もが彼に相談に行く.厳しい反対者でさえ認めるくらいの理論が作れれば理論は完成したと見ていい.それほど彼は信頼されていた.彼は目立たないところにいたが常に量子力学建設の中心人物の一人だったのだ.
いや待てよ,本当に中心だったかなぁ……?脇の方でボーアとアインシュタインが論争していてくれたお陰で,他の人たちが自分の研究に集中できたという雰囲気も感じないではない.
彼は量子力学に弱点を見つけた.理論にほころびがあると指摘した.多くの人がその点を修正してより良い理論を作ろうと思った.一方,無視して理論を発展させることに集中した人も多くいた.
EPRパラドックス
その弱点を指摘した論文は弟子たちと連名で発表したため,「アインシュタイン・ポドルスキー・ローゼンのパラドックス」と呼ばれている.頭文字だけを取って「EPRパラドックス」と呼ぶことが多い.1935 年の発表だから,量子力学の基礎的なところはほとんど完成しており,議論がかなり落ち着いた頃の話だ.その論文に書かれている哲学的意味はとても深いのだが,そこを省いて興味あるところだけを要約して,さらに現代の視点で解釈し直せば(……やりすぎか),次のようなとても簡単な話でしかない.
もともとスピンが 0 である粒子が反応して,結果,スピンを持つ粒子 2 つが一度に生成されたとする.この粒子のスピンが上向きか下向きかは測定するまで分からないが,一方を測定して上向きだったなら,もう一方は必ず下向きである.そうでなければ角運動量保存則に反するだろう.
量子力学では測定するまで結果が単に分からないというのではなく,状態がどちらとも定まっていないと主張しているのだった.しかしこの場合,一方の粒子を測定して結果を知ってしまうと,もう一方は測定しなくても状態が定まってしまっているという奇妙なことが起きている.一方の粒子を測定した事の影響がどのようにして他方に伝わるというのだろう.これがアインシュタインの疑問だ.
光の速さより速く情報を伝える具体的な仕組みがあるのだとしたら相対性理論に反する.しかし一方を測定したという情報が無限の速さで伝わるのでない限り,角運動量保存則に反する事態が起こり得るのではないだろうか.例えば二人の観測者が,互いに離れ去ったペアの粒子をそれぞれの場所で測定するとき,一方での観測結果が他方に伝わる前にもう一人も観測してしまったとしたら…….量子力学の解釈ではそれぞれの観測結果は確率で決まるというのだから,両方ともがスピン上向きの結果を得るなんてことも起こってしまうのではないだろうか.すなわちこれはパラドックスである.
大切な注:原論文ではこのことがもっと数学的に記述されている.だからこそ多くの学者が彼らの意見を放っておくわけにはいかなかったとも言える.その論文にはスピンの話なんかは出てこなくて,波動関数による抽象的な議論に終始している.例として精々位置や運動量が出てくるくらいだ.
この話がスピンの話と結び付くのはもっとずっと後の事であり,アインシュタインの主張を確認する現実的な手段としてボームにより提案されたのが 1951 年のことだ.しかしその提案当時でさえ,それはまだ思考実験に過ぎなかった.
思考実験
相対論が破れているのか,角運動量保存が破れているのか,それとも量子力学の解釈が間違っているのか.これを実験で確かめるのは簡単ではなかった.思考実験なら簡単だが,具体的な手段を考え始めるとすぐに壁にぶつかる.
一組のペアだけを作り出す技術.生成した粒子に影響を与えることなく,待ち構えている検出器へとまっすぐ導く技術.1粒子のスピンだけを検出する技術.これらは非常に難しい.だからと言って多数のペアを作れば,どの粒子とどの粒子がペアなのか分からなくなってしまう.しばらくは思考の中だけで実験を続けるしかない.
ペアで生まれた粒子が測定されないまま,銀河の端と端に到達したとする.一方で博士 A がそれを測定したら,スピンは上向きだった.それを見ていた妖精ティンカーベルは,光のような速さでもう一方の粒子を追いかける.その向こうでは別の博士 B がその粒子を測定しようと待ち構えていた.ティンクはニヤニヤしながらそれを見ている.「測定するだけ無駄よ.その結果はスピン下向きになるわ.」結果はその通りになった.これは当たり前の話だ.博士 A が測定した時点で,もはや確率なんて関係なかったのだとティンクは思った.
しかし博士 B はこう考えた.私はティンクが言うのを聞いてしまった時点で観測したことになるのだ.私は「スピン下向きになるわ」と話すティンクと,「スピン上向きになるわ」と話すティンクのどちらに出会う可能性もあったわけだが,たまたま確率的に前者に出会ったわけだ.
別のケースを考えてみよう.博士 A が測定をしてスピン上向きだった.ティンクは光のような速さでもう一方の粒子を追いかけたが,着いた頃にはすでに博士 B はその粒子を測定し終わっていた.博士は言った.「5万年前に測定は済んだよ」こういう常識外れの寿命の博士が登場できるのが思考実験の利点だ.ティンクは考えた.「博士 A が測定してからその情報がここに届くのだとしたら,光の速さでも10万年はかかるはず.それ以前に測定しちゃったのだから結果はどうなるの……?」博士は答えた.「スピンは下向きだった.そして博士 A は上向きを観測したんだろ?そうだね?」ティンクはそうだと言った.博士は満足げだ.
博士はこう考えた.私は確率的にスピンを観測した.博士 A の測定とは関係ない.観測するまでは粒子の状態は定まっていなかった.しかし私がスピン下向きを観測した時点で,博士 A がスピン上向きを測定したことを証言するティンクがやがて来るだろう事が確定したのだ.それまではどちらのティンクも私の元へ来る可能性があったのだ.
思考実験はここまでにしよう.以上が量子力学的な考え方だ.しかも相対論に矛盾するような考え方も避けているのが分かるだろうか.情報が光より速く伝わったとは考えていないのだ.量子力学に間違いがあるなどと言えるだろうか.矛盾なんてどこにもないのだ.
しかしこの解釈が正しいかどうか知る方法がない.そこでアインシュタインは考えた.こんな奇妙な考え方をしなくても,粒子が生成された時点ですでにどちら向きの粒子として観測されるかが決まっているのではないか.そう考えても同じ結果を説明できるではないか.粒子の内部にはまだ知らない変数があって,それが測定結果を決めているはずだ,と.
この考えに影響され励まされた人が多くいたため,しばらくの間,「隠れた変数理論」の追求が流行ることになる.
追記(2024/01):ここで妖精ティンカーベルが出てくるのは,どうやら「ベルの不等式」のベルと「ティンカー・ベル」のベルを懸けているようなのである.自分でも忘れていたというか,本当にそういう意図だったのか覚えもないのだが.
ベルの不等式
この議論は 30 年近く続いた.隠れた変数理論を見つける努力も続いた.実験で確かめる方法がない以上,なかなか決着の付く話ではなかった.理論というのは実験がなければ無力なものだ.しかし 1964 年,この問題に決着を付ける手掛かりがベルにより提案されたのだ.
これから紹介する「ベルの不等式」と呼ばれるものには幾つかのバリエーションがある.CHSH 不等式なんていう,数学的にもそれほど難しくなく,より深い見方ができるものもあるのだが,ここで説明するにはちょっと堅苦しい.興味のある人は他の教科書をあたってもらいたい.ここでは電子のスピンを使った一番納得し易そうな形のものを紹介することにしよう.
追記(2014/10):その後,CHSH不等式についての解説も追加しておいたのでこの次の記事も続けて読んでみてほしい.
追記(2014/10):ベル本人によるオリジナルのベルの不等式の解説記事もその次に追加しておいたので参考にしてほしい.
追記(2024/01):以下の説明は私が学生の頃の「集中講義」の際に黒板を手書きで写したノートを元にして書いたものである.学外から企業研究者の方を招いて行われた授業だったのだが,どうやらその元ネタとなる論文があるらしいというのを数年前に知った.今回ちゃんと明記しておこうと思って探してみたのだが,実は論文ではなく,海外の入門教科書的なものかもしれない.
(日本語版)『量子論――幻想か実在か』(1987) A.I.M.レイ著(林一訳)
(原著)『Quantum Physics: Illusion Or Reality?』(1986) Alistair Rae
追記(2024/11):『現代の量子力学(上)』(J.J.サクライ著)にも同じ解説が載っていることに気付いた.そこには「E.P.ウィグナーによって考案された簡単なモデル」と書かれているので,そちらが元ネタであろう.しかしウィグナーによる論文は私には見付けられなかった.
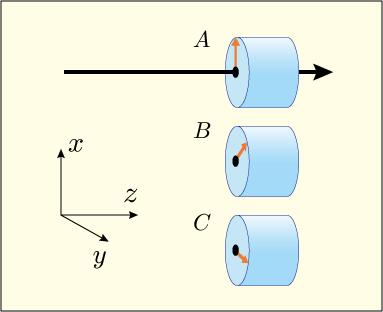
まず,次のような 3 種類の測定を考えて,それぞれを A,B,C と呼んで区別しよう.測定 A は軸方向のスピンを測るもの.測定 B は
軸に対して角度
だけずらした軸でスピンを測るもの.測定 C は
軸に対して角度
だけずらした軸でスピンを測るもの.つまり前に出てきたフィルター装置を回して,通過するかどうかを見るわけである.
量子力学では測定するまでは結果は定まっておらず,測定の瞬間に確率によって決まると主張しているのだった.しかし今はこの考えに真っ向から対立する仮定を置こう.粒子は生まれた瞬間に次の測定でどんな結果になるか,すでに決まっているのだとする.それを決めるような変数が粒子の内部にすでにあるというわけだ.
つまり測定 A を行った場合に上になるか下になるかが予め決まっており,もし測定者が気まぐれで代わりに測定 B を行ったとしても,その結果が上になるか下になるかは,予め決まっているとする.測定 C についても同じである.
誤解のないように注意しておくが,どの測定をしても同じ結果が出ると言っているわけではない.どの測定をしたらどの結果が出るかが予めすべて定まっていると言っているのだ.
さらに注意したいのは,2 つ以上の測定を連続して行うようなことは考えていないということだ.一つの測定をした結果,内部で設定されている変数が変化してしまう可能性はある.これを否定する仮定をすべきではない.
ここでは A, B, C の 3 つの測定だけを用意したが,それ以外の無数の角度について測定をしたときにどんな結果になるかについても予めすべて決まっているというのが,この仮定をした思想である.だから粒子の内部に存在する変数は非常に複雑な仕組みになっていることが考えられる.ひょっとすると量子力学の構造を再現出来るかも知れない.それがどんなものであるか想像も付かないが,そのような泥沼に足を突っ込む必要はない.次のような簡単なことを考えればいい.
あらゆる内部状態は,次のような単純なグループに分類する事ができる.つまり測定 A をしたら 上になるグループと下になるグループ.そしてそれぞれのグループの中で,測定 A をしないで代わりに測定 B をしたら上になるグループと下になるグループを分けることが出来て,全部で 4 つのグループになる.さらにそれらの中で,もし代わりに測定 C をしたら上になるグループと下になるグループを分ける.こうして全部で 8 つのグループが出来る.
粒子は生まれた瞬間にこの 8 つのグループのいずれかに属すると言えるわけだ.これらのグループに名前を付けよう.左から順に測定 A, B, C に対する結果を書いて
と表しておけばいいだろう.
はグループの頭文字だ.
さて,ここで,ペアとなる粒子を同時発生させることを考える.先ほども話したように,元々角運動量が 0 であるような粒子が崩壊して二つの粒子となり左右に飛んでいくような状況を考えれば良いだろう.それらの両方を先ほど考えた A, B, C のいずれかのフィルター装置に通してやる.右と左で同じ角度の装置に通す必要は無くて,それぞれ異なっていても良い.
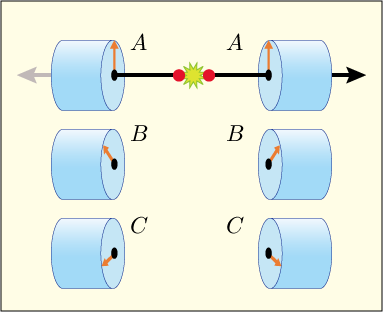
同時に生成された二つの粒子が角運動量保存則を満たすためには,一方が例えばに属するとすると,もう一方は必ず
に属することになる.どんな測定に対してもかならず一方とは反対の結果が出なければならないからだ.
もし一方の粒子に対して測定 A を行って上向きという結果が出たとしたら,他方の粒子は測定するまでもなく測定 A に対しては下向きとなる.つまり他方の粒子は,
,
,
の 4 つのうちのいずれかに属していることになる.
さらに別の状況を考えてみる.一方の粒子に対しては測定 A を行ったが,他方の粒子に対しては測定 A を行うのではなく,代わりに測定 B を行ったとしよう.その時に結果が上となったとしたら,その他方の粒子はと
のいずれかまでは分からないが,とりあえずどちらかに属するものだったとは言えるわけだ.
では,このことを踏まえて,量子力学と比較することのできる式を導き出してみよう.
今から回の実験をするとする.このとき,一方の粒子が 8 つのグループの内のどれに何回属することになるかを,それぞれ次のように表すことにする.
これら全てを合計すると
になるわけだ.
を非常に大きくすると,各グループの
の値の割合はだいたい
や
の値によってのみ決まることになる.あらかじめ内部状態が何らかの状態に決まっているのだから,
を大きくすればその割合についてもこのように分類できるはずである.残念ながら毎回の測定によってその粒子がこれらのいずれに属するかは完全には判定できない.ではどうやって数えたらいいのだろうか.
実は数えないのである.この考え方を使って確率を計算してやることにしよう.一方の粒子で測定 A をして上向きで,かつ他方の粒子に対して測定 B をして上向きであるような確率は次のように表せる.
なぜなら,他方の粒子での測定 B が上向きなのだから,最初の粒子に対してもし測定 B をしていたら下向きであるはずで,これで最初の粒子の状態は A に対して上向き,B に対しては下向きであることが確実である.C に対しては分からないが今回の確率を知るためにはどちらでもいいから両方の可能性を計上しておいたという具合である.
同じようにして,次の関係も言える.
この 3 つの式を見ると,最後の式の右辺にある
と
とは両方とも前の 2 つの式にも含まれていることに気が付くだろう.つまり,
という関係が成り立っていると言える.そして右辺に余っている
と
はいずれも正の値なのだから,
であることが言えるのである.これが「ベルの不等式」だ.これは粒子が生まれた時点で 2 つの粒子の状態が予め定まっていると仮定したことによって導かれた式であり,それ以外の仮定はしていない.この不等式にどんな使い道があるだろうか.
アスペの実験
量子力学はこの不等式を満たしているかを考える.計算し易いようにという条件で計算してみよう.つまり測定 C は測定 B の 2 倍の角度を回して行うものと仮定する.もう一度分かりやすく言い直せば,
である.
まずはから考えて行く.初めに測定 A を行って上向きになる確率は 1/2 である.ここでは量子力学的な深い理屈はそれほど関係なくて,ペアの粒子が生成された時,それがどんな重ね合わせ状態にあるかは特に偏りがなく,ランダムだと考えられるからである.多数の実験をすれば上が出る確率と下が出る確率は半々となるであろう.
この初めの測定により一方が上向きだと確定すれば,他方の粒子はなぜか自動的に下向きであることが確定したわけで,もし測定 A を行えば,上向きになる可能性は 0 だろう.しかしそこからだけずらして測定を行えば,
の確率で上向きが観測できることになる.つまり,
である.
追記(2024/01):ここの部分について「誤植ではないですか?」という問い合わせがよくあるので説明を加えておこう.この計算の根拠は 4 つほど前の「スピノル(イメージ重視)」という記事の一番最後に書かれている結論を使っている.そこではという結論になっているが,それは同一の粒子を連続して二つめのフィルターに通すからである.今回は最初のフィルターを通った粒子とはスピンが反対向きになっている「他方の粒子」を使うので,確率が逆転しており,
つまり
となる.また,「
ではなく
ではないですか?」という問い合わせもよく受けるが,おそらく光の偏向の話と混同していると思われる.光は偏光フィルターの向きを 90°ずらせば通り抜ける確率は 0 になるが,今回は電子などのスピンで考えているので 180°ずらすことで 0 になったり 1 になったりするのである.
同様にして,
である事も導かれる.これらを先ほどの不等式に代入してみよう.
さらに
という仮定をここで使うことにする.
結果は次のようになる.
これが意味するのは,量子力学の予想においても
がこの条件を満たす範囲内でなら,先ほどの不等式がちゃんと満たされているということである.よってそのような範囲を調べても面白い事は何もない.しかしこの範囲を越えたところで実験して結果を比較してやれば量子力学と隠れた変数理論の違いが見付けられるはずだ.量子力学は
の範囲,あるいは
の範囲でベルの不等式を破る!このような角度設定で重点的に調べればいい.さて,どちらがより正しい理論だと言えるだろうか.
追記(2024/01):現代の視点で書けばこの時点で「量子力学はベルの不等式を破る!」と言って終わりにすればいいのだが,この記事は当時の雰囲気を重視して書かれている.この当時,まだ量子力学の実験的検証は十分ではなく,特に今回の思考実験のような量子もつれの実験は行われていなかったのである.
それは 1982 年にアスペらの実験によって明らかにされた.ベルの不等式発表からさらに 18 年.かなり最近のことなのだ……少なくとも私にとっては.何と,ベルの不等式は成り立っていなかった!類似の実験は他に幾つも行われたが,やはり同様の結果だった.
追記(2024/01):実はアスペらの実験はこの記事で説明したタイプのものではなく,もう少し洗練されたタイプのものである.今回説明した実験をやろうとすると,左右で全く誤差なく同じ角度に設定したフィルターの対を用意しなければならないだろう.少しのズレがあるだけでも粒子内部の隠れた変数の働きが大きく違ってくる可能性があるという批判の余地が残るからである.そんな実験は現実的に無理であり,その弱点を克服したのが次の記事で説明するCHSH不等式である.アスペの実験ではその破れを実験的に検証した.
量子力学は正しかった.角運動量保存則も破れていなかった.では相対論が間違っていたのかというと,前に話したようにこれは相対論に矛盾を起こすようなものでもない.隠れた変数が存在するという仮定のもとでは説明の付かない現象が現実に起きていることがはっきりしたということだけである.
こうして量子力学は「隠れた変数」理論よりも広範囲に現象を説明することのできる優れた理論であることが認められることになった.そして「隠れた変数」を探す試みは下火になった.
そう,下火になっただけである.ごく一部の人々がベルの不等式に引っ掛からないような形の隠れた変数理論が作れないものかと今日も頭を悩ませていることだろう.がんばれ,アインシュタインの正統な後継者たちよ.こんな風に煽って若い読者を不毛の荒野へと誘うのは非常に無責任なのだが,そこに何もないとは言い切れない.
今ではアインシュタインの提議した問題はパラドックスには当たらないという理解に達しており,「EPRパラドックス」という言葉はあまり使われなくなってきている.代わりに「EPR相関」という用語が広く使われるようだ.
舞台裏に何がある
我々の生存,いや我々だけでなく,全ての存在の舞台となっているこの宇宙.その舞台裏に,離れた 2 点間の状態を「同時」に操る仕組みが存在している.この「同時」というのは,我々が考える時間の概念を超越した意味での「同時」だ.なぜなら時間は,現在の理解の枠組みでは,この宇宙という舞台の一部であるから.
それらを含めた舞台の裏に何かがある.そういう意味での隠れた変数(仕組み)が存在する事はまだ否定されていない.何かの発見がきっかけで舞台裏が明らかになり,改良されたエーテル的な理論が主流になることだってあるかも知れない.
エーテルを口にする者をそのことだけで疑似科学者と決め付け,相対論は絶対的に正しいなどと盲信し主流派に紛れていい気になっている「科学フリーク」たちは,その時に自分の馬鹿さを見ることになるだろう.自分の馬鹿さに気付けば良いが,おそらく「世界が自分を裏切った」のだとまた誤解するのだろう.
真っ当な科学者は,自分はエーテルとは関係ないよ,と涼しげな顔をしながら,いつでも世界観を覆す機会を狙っているものだ.ただ現在のところ,エーテル説を主張する人々の中に,注目に値するまともな論理は見当たらないように見える.
アスペがエーテルのことを少し口にしたというくらいの事で,相対論否定論者は自分の手柄のように喜ぶな,騒ぐな,勝ち誇るな.恥ずかしいから.
追記(2024/01):ここでやたらと口調が荒々しいのは,当時のネットでは「相対論は間違っている」と主張する人々の活動が今よりもずっと活発で,集約された形のSNSなどというものはまだ無く,あちこちのネット掲示板にゲリラ的に現れる彼らと日々闘っていたからである.
多くの科学者がエーテルという言葉そのものにやたら神経質になっているのは,エーテルと口にする人全体の平均レベルが非常に低いからだ.エーテルが好きな人は足を引っ張らないで,エーテル説とは無関係なフリをして生活していてほしい.できるなら静かに勉強していつか世界最高のレベルに到達した後で,誰にも簡単には否定されない論理で世界観を覆して欲しいと思う.
私はエーテル好きだが,自分は十分に足を引っ張るレベルにいることを自覚している.だから主流派のふりをして主流派の中に紛れ込む.私のしっぽはたまに見え隠れする.
個人的な思索
私は物理を離れたところでふと思う.
私は宇宙の片隅にいるちっぽけな存在に過ぎないが,私が取った行動,決断,思いの全てが,即座に全宇宙のあらゆる場所に何らかの影響を与えているのではないだろうか.この宇宙は巨大で複雑な「生き残り頭脳ゲーム」のようなもので,私は普段の生活で何の気も無しに重要なレバーを引っ張っていることがあるのかも知れない.
あるいはこんなことを思ったりする.
私は今ここにいて,この小さな身体が私の全てだと思っているが,この私という存在は,全宇宙が複雑な組み合わせによって,この場所に作り出した影のようなものに過ぎないのではないだろうか.私をここに生かすために全宇宙規模で複雑な計算が行われている.私の本体は全宇宙であり,私の意志はどこか別のところで全宇宙を用いて決定されているのかも知れない.
こういうことは心の片隅に置いておいて,さあ,物理に戻ろう.
修正履歴
(2014/10/13)
・CHSH不等式の記事が追加されたことを追記.
(2014/10/17)
・オリジナルのベルの不等式を解説する記事が追加されたことを追記.
(2024/01/19)
・記事中に出てくる駄洒落の自己解説を追記.
・この記事の元ネタとなっている出典を現在分かる範囲で追記.
・実験の説明図を二つ追加.
・よく質問が寄せられる部分について詳しい補足説明を追記.
・計算の途中式を追加.
・結論近くの話の流れの分かりにくさを解消するための追記.
・アスペらの実験が実は今回の説明で紹介したものとは異なるCHSH不等式の検証であることを追記.
・記事中の口の悪さについての弁解を追記.
・本文のあちこちを分かりやすくわずかずつ修正.
(2024/11/29)
・この記事の元ネタとなっている出典を現在分かる範囲で追記.










