量子力学：スピンの振る舞い

状態の重ね合わせ

理論の抽象度が増してきたので,読者がついて来れているか心配である.ちょっと急ぎ過ぎたと思う箇所もある.読者を過小評価するつもりはないが,なるべく多くの人に先の方まで読んでもらいたいと考えているので,念のため,具体的な実験結果との対応をきちんと確認しながら進むことにしよう.（すでに第 2 部の摂動論辺りでかなりの脱落者を出している気もするが……）

前回,軸方向にスピンを測定した時の「上向き状態」と「下向き状態」をそれぞれ, |↑>} と |↓>} という記号で表した.しかしスピンは他の軸で測っても ±ℏ/2 の二通りの値しか取らないのだった.これは前回の計算でも導かれたし,そもそもどの方向も対等であるはずだから当然の結果ではある.

だから軸だけを特別扱いしないで,他の軸に沿って測定した後の状態も同じような記号を使って表してやりたい.そこで, |x↑>} だとか, |z↓>} だとかいう記号を導入して,どの軸について測定した後の状態であるかも同時に表すようにしよう.

注意：これらの記号はこのサイトだけの約束であるから,どこでも説明なしに通用するものだと思ってはいけない.しかしこれくらいのものなら,いきなり使ったとしても頭のいい人たちはすぐに分かってくれるだろう.

独り言：記号というのはお互いの間で意味が通じればいいのであり,作法をあまり気にしていてはいけない.最先端に近付くほど,記号の使い方はバラバラだったりする.異なる記号体系で書かれたものの意味を瞬時でつかみ取る才能が求められる.記号法が統一されるのは議論が落ち着いて十分な時間が過ぎてからのことだ.記号の違いに一々驚いていてはいけない.「こう書かないと間違い」などと些細な決まりをうるさく言うのは義務教育の間だけでいい.もちろん,論理的に欠陥のある書き方を許していいという意味ではない.

前回の結果を再確認しておくと,各状態は次のように表せるのだった. これは初めに |z↑>} や |z↓>} をなるべく簡単になるようにと考えて 1 と 0 で表しておいたからこのような表現になっているだけであって,これらをユニタリ変換したものを使っても理論的には同等である.それについては次回で議論することになるだろう.とりあえず,この形式だけが唯一絶対というわけではないことだけは頭に置いておこう.

さて,これらを見ると, という関係があることがすぐに分かる.これが意味するのは,x 軸方向にスピンを測定して「上向き」であることが確実となった後の電子の状態というのは,軸方向での「上向き」と「下向き」が半々に重なった状態であり,もし次に軸方向のスピンを測定したならば「上向き」と「下向き」が半々の確率で表れるだろうということだ.

また,次のような関係も同じくらい簡単に見出せる. ここで右辺第 2 項目の係数が負になっているからと言って,ややこしいことが起きているわけではない.本質は先ほどと何も変わらない.これはベクトルの重ね合わせであるから,ベクトルを重ねる時の向きが先ほどとは違うというだけである.確率の比較は係数の「絶対値の 2 乗」の値を使って行うので,係数が負であることの影響はない.

各係数の絶対値の 2 乗の和を取ったものは全確率であって,ちゃんと 1 になるように出来ている.各状態ベクトルの大きさを 1 に規格化しておいたのはこのためでもある.

さて,ここまでは |z↑>} と |z↓>} を使った重ね合わせで解釈してきたが,同じ状態を次のように |y↑>} と |y↓>} の重ね合わせとして表す事も可能である. 係数が少しだけ複雑な形になっているが,これらの絶対値の 2 乗を計算するとそれぞれ 1/2 となっており,確率的に半々の重ね合わせとなっていることが分かる.

この係数を求めるのは簡単である. |x↑>}=a|y↑>}+b|y↓>} と置いてやり,これに左から <y↑|} を作用させれば, となる.同じように左から <y↓|} を作用させればになる.つまりという具合に内積を計算してやればいいのである.

全ての軸は対等であるから,同様の関係は他にも見つけられる.軸での「上向き」「下向き」を |x↑>} と |x↓>} の組で表したり, |z↑>} と |z↓>} の組で表したり出来る.軸での「上向き」「下向き」を |x↑>} と |x↓>} の組で表したり, |y↑>} と |y↓>} の組で表したりも出来る.

要は,ある軸に沿ってスピンを測定して結果が出た直後の粒子を,次にそれとは直角になる方向に測定すると,結果は半々の確率でどちらかに決まるということだ.

集団での振る舞い

粒子のビームを使って考えよう.ビームの進行方向を z 軸とする.前回のシュテルン・ゲルラッハの実験装置を使って軸方向にスピンを測ると,結果としてビームは二通りに分かれるのだった.ただし前の状態が分からないからどんな割合で分かれるかは不定である.

この後,分かれた内の一方のビームだけを使って,今度はこれを軸方向の測定をするための磁石に通せば,これもさらに 2 つに分かれるのである.しかもこの度はどちらへ進むかの確率は完全に半々である.個々の粒子がどちらへ進路を曲げるかは確率でしか言い当てられなくて,理論としてはとても頼りないことだが,集団として見れば,ほぼ正確に半分の粒子が上向き,そして半分が下向きとなるということが,確率ではなく,確実に言える.

ところで測定する度にビームの方向が少しずつ曲がってしまうのは,ちょっと厄介である.ビームの方向に合わせて測定装置を斜めに配置すると,軸や軸に沿って測定しているとは言えなくなってきてしまうからだ.

追記(2024/01)：実際のシュテルン・ゲルラッハ装置では磁石の部分から数十センチほど離れた標的のところまで粒子が飛ぶ間に1mm程度の差が出るくらいでしかないので,粒子の進路が元の角度から逸れることについてはあまり気にしなくても構わない.しかしそれは銀原子が重すぎるからその程度のズレしか生じないのであって,代わりに電子を飛ばす場合にはもっと大きく逸れる可能性がある.実際にそこまで気にして説明している教科書は少ないが,やはり気になる人は多いだろう.

上の例ではまだこの点について問題は無かった.しかしこの後の話では問題が出てくる.そこで次のようなアイテムを導入しておこう.

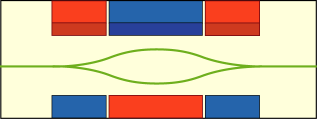
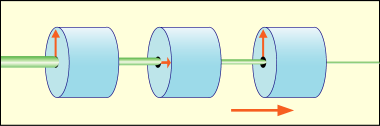
3 つのシュテルン・ゲルラッハ磁石を向きを反転させて交互に配置する.こうすることで 2 つに分かれたビームを再び元の進路に戻すようにするのである.装置の中間地点辺りのビームが 2 つに分かれたところで一方を遮ってやるような細工をしておいてやると,

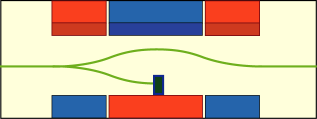
これは測定方向のスピン成分が「上向き」「下向き」のどちらかになっている粒子だけの通過を許す「フィルタ装置」として働くのである.上のような図を毎回描くのは面倒なので,これをシンプルなケースに入れて使う事にしよう.

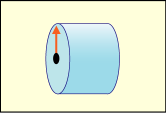
矢印はスピンの向きを表している.上の図のような磁石の配置の場合,上側のコースを通るものが「スピン上向き」になっている.

測定による状態変化

このフィルタ装置を使って「x 軸上向き」だけのビームを取り出そう.そのビームを再び「x 軸上向き」を取り出すフィルタに通したらどうなるか.100 % が無事に通過するのである.一度軸上向きである事が確定した粒子は何度同じ測定に掛けようとも,x 軸上向きである事実は変わらないのである.これは,「測定の時には原理的に何かをぶつけなければならないから,その反動によって測定値が確率的に揺らいでしまう」なんて説明が適切でない事がはっきり分かる好例だ.

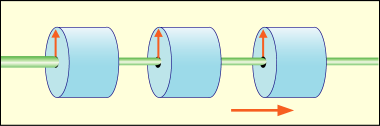
粒子を3つのフィルターに連続して通すが、最初のフィルターで半分になったあとは少しも遮られないで出てくる様子を描いた図

ではこのビームを「軸上向き」だけを通すフィルターに入れたらどうなるか.先ほど考えたように,50 % だけが通過する事になる.つまりビームは弱くなって出てくる.

ではこれをもう一度「軸上向き」を取り出すフィルタに通したらどうなるか.これがスピンの面白いところだ.先ほどまでは確かに全ての粒子が「軸上向き」だった.しかし今回は全てが通過するのではなく,ビームはさらに半分になるのである.半分が「軸上向き」,半分が「軸下向き」となってしまった！軸方向に測定した時点で,それ以前に軸方向に対してどちら向きだったかは関係なくなってしまう.

向きを変えた3つのフィルターに粒子を連続して通したときに、毎回半分に減って出てくる様子を描いた図

測定によって状態が変わるというのはこういうことなのである.演算子が交換しないような物理量を測定する場合,最後の測定結果こそが全てであり,それ以前の状態は測定によって「御破算」になってしまうのだ.

スピンは電子固有の性質

シュテルン・ゲルラッハの一番初めの実験では銀原子のビームが使われた.これは賢い方法で,後でターゲットを取り出して観察することで結果を正確に判定することが出来る.

しかしその後には細く絞った電子ビームを使って同じ事が確かめられるようになってきた.電子ビームというのはつまり「陰極線」のことであって,中学や高校の実験室にでも発生装置が置いてあるだろう.非常に手軽なものだ.電子の到達点を精度良く測れるような装置も工夫されてきた.また先ほど導入したようなフィルター装置を使えば,電流量を測ることでフィルター装置を抜けてくるビームの強度が分かるのでもっと簡単だ.

ただし電子を磁場中に通す時には,電気的に中性の原子を使う時とは違ってローレンツ力が働く.ビームが余計な方向に曲がろうとするので,フィルター装置の設計をする時に少々面倒な要素となりそうだ.また電荷が力を受けて進路を曲げられる時には,制動放射が生じるだろう.つまり量子論的には光子を放出することに相当するのではないだろうか.このことが電子のスピン状態に影響を与えてしまう心配があるが,それについてはこの段階の知識では論じる事が出来ない.

制動放射の原因はローレンツ力だけではなかった.スピンと磁場の作用によって電子のコースを曲げるという,この実験の中核となる部分でも同じ問題が発生する.これは中性の原子を使った時には気にしなくて良いことだった.

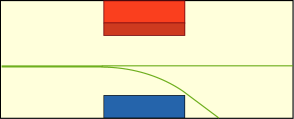
しかしその心配はちょっとした工夫で回避できそうだ.電場を使えば電子ビームの曲がり具合を補正してやることが出来るので,ローレンツ力との釣り合いを取ってやれば,電子を真っ直ぐ進ませる事が出来る.また上と下に分かれて進もうとするところに電場で偏りを掛けてやり,一方を真っ直ぐ進ませ,もう一方をより強く曲がるようにさせる.こうして真っ直ぐ進んだビームだけを取り出すようにすればいい.これで制動放射を生じさせないで済むし,磁石を 3 対も使わなくても済む.万事解決だ.

とにかくこうして,電子のみを使ってもスピンが測定できるということは,スピンの作用は原子核の周りを回っているかどうかに関係ないということだ.スピンというのが電子単独の性質である事が分かる.これはスピンの正体が電子の自転であるとする見方に近い性質だ.一体,電子は波なのか,粒なのか.本当にイメージしにくい.

角度を変えるとどうなるか

こういう手軽なフィルター装置があると色々なことを試したくなる.

一度「軸上向き」フィルターを通ったビームは,同じ向きのフィルターを何度通っても100 % 通過するのだった.また,そのフィルター装置を 90°ずらして「軸上向き」フィルターとして使用すれば,50 % が通過するのだった.では角度を90°ずらすのではなく,ほんの少しだけずらした場合にはどうなるのだろうか.

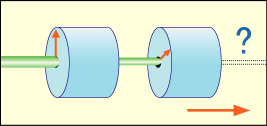
2番め以降のフィルターの角度を少しだけ変えたときにどういう結果になるかを問題提起する図

いきなり状況が全く変わってしまうなんてことは考えにくい.角度が小さい内はほぼ100 % に近い粒子がフィルターを抜けてくるだろう.そして角度を徐々に増やすにつれて通過率はだんだんと下がってくるのではないかと予想される.90°回して 50 %,180°回せば 0 % だ.しかし途中が気になる.角度に応じてフィルターを通過する確率はどのように変化するのだろうか.

そんなものは実験をすればすぐに分かることだが,理論的に示せてこそ,ちゃんと理解した気になれるというものだ.それを次回のテーマにしよう.

修正履歴

(2024/01/13)
　・実際のシュテルン・ゲルラッハ装置での粒子の進行方向の変化は極めてわずかであるというコメントを追加.