量子力学：スペクトル項

スペクトル項とは何か

スペクトル項というのは,現代的な見方をすれば要するに「エネルギー準位」のことであるが,歴史的な経緯でこう呼ばれている.まずはその辺りを説明しておこう.

我々はエネルギー準位を直接見ることは出来ず,そのエネルギー準位間の状態変化があったときに飛び出してくる光子を観測することになる.光をプリズムで分解したときの七色の光の帯をスペクトルと呼ぶのだが,調べたい物質を少しだけ混ぜた真空管の中で放電をさせたときに出てくる光を分解すると連続的な色の変化ではなく不連続な幾つもの線が見られる.そのパターンは物質によって異なる.そういうものを細かく分類して研究してきた長い歴史があるわけだ.我々が直接調べることが出来るのはそういう光の波長である.

二つのエネルギー準位 E_m > E_n があるときに出てくる光の波長は次のように表せる. まだエネルギー準位という考え方が確立していない時代に,波長の逆数はどれも何らかの「謎の量」の差によって表せると気付いたのだった.現代的には上の式を少し変形して次のように表せる. この右辺で使われる項のことを「スペクトル項」と呼んだのである.

我々の先輩科学者たちは,この理論上の謎の量であるスペクトル項を見つけては分類するという地道な作業を行わなければならなくなった.そのための分類記号を発明する必要があったのである.それが「スペクトル項記号」あるいは「項記号」と呼ばれるものである.現代的には,様々なエネルギー準位に付けられた呼び名であるという理解で良い.

項記号の意義

水素原子だけならエネルギー準位の数も多くはなく,わざわざ名前を付けるほどでもなかっただろう.バルマー系列やライマン系列やパッシェン系列などの発見の歴史は高校でも習うことだろう.つまり,主量子数の違いだけでおおよそ分類が可能である.

水素でも外部から電場や磁場を掛ければ角運動量の違いによってエネルギー準位が分裂する（微細構造）し,原子核とスピンとの相互作用によってもさらに僅かな分裂が発生している（超微細構造）のだが,それは今は置いておこう.特に超微細構造については化学的な結合を説明するためには必要ないので今後もそういう細かい話は無視し続けるつもりである.

ところが多電子原子になると話は複雑である.複数の電子の「軌道角運動量やスピン」の相互作用によってエネルギー準位の差が生まれる.スペクトルには密集した細かい多数の線が現れる.その全てを分類せねばならない.つまり,観測によって発見された様々な励起状態のエネルギー準位について,その時の電子状態が一体どうなっているかを特定しないといけない.

とは言ったものの,原子の構造がはっきり分かってきた現代では話が逆になってきており,考えられる電子状態を効率よく全て書き出すために項記号が使われ,そのそれぞれの状態のエネルギー準位を計算で導くことの方が関心の的になっている.

例えば p 軌道で何が起きているか

項記号を具体的にどう書くのかという話はもう少し後にして,まずは状況を説明したい.

例えば p 軌道には m=1,0,-1 の 3 つの状態があり,そのそれぞれでスピンが上向きと下向きの 2 つの状態があるので,合計 6 つの状態が存在している.

m=1		m=0		m=-1
↑	↓	↑	↓	↑	↓

とりあえず簡単な例として,この p 軌道に電子が 2 つだけ埋まっている状態を考えよう.

電子は互いに同じ状態を取れないので 2 つの電子はこの 6 通りの中からそれぞれ異なる状態を選ぶことになる.その組み合わせは _6C_2=15 であるから 15 通りの電子の収まり方があるというわけだ.

	m=1		m=0		m=-1
[1]	↑	↓
[2]	↑		↑
[3]	↑			↓
[4]	↑				↑
[5]	↑					↓
[6]		↓	↑
[7]		↓		↓
[8]		↓			↑
[9]		↓				↓
[10]			↑	↓
[11]			↑		↑
[12]			↑			↓
[13]				↓	↑
[14]				↓		↓
[15]					↑	↓

この 15 通りの中でどのような入り方をしているときが一番エネルギー準位が低くて安定しているかというのは今回の主題ではない.真空放電の中では激しい衝突が繰り返される結果として状態が次々と変化しており,これら 15 通りのどのような状態も取り得る可能性がある.どの状態も現実的に存在し得ると考えられるわけだ.

ところで前々回の記事で磁気量子数の違いによってはエネルギー準位に差が出ないと言う話をしたことを覚えてくれているだろう.しかし今は磁気量子数の違いによってエネルギー準位に差が出るようなことを話している.これは矛盾しているのではないかと思う人もあるだろうが,そうではない.

原子の内部的にはそれぞれの電子の軌道角運動量やスピンの向きによってエネルギー準位に差が出る.つまりそれらが互いに同じ向きを向いているか,逆向きになっているか,あるいはそのどちらでもなくどこか別方向にずれているかというのはエネルギー準位の違いをもたらす.その指標として仮に軸方向について測定した時の成分を表す量子数使って互いの向きの関係を区分しているだけのことである.

そう思って上の表を眺めてみると状態 [1] と状態 [15] は実は同一の状態を意味しているのであって,同じものを上下逆に見ているだけであることが分かる.ある方向から見る限りではこれらはもちろん別々の区別できる状態なのだが,どちらも状況は似たようなものだという意味である.つまり少なくともこの 2 つはエネルギー準位的には違いがないので同じ項記号を割り当てられるべきであろう.他にこれらと同じ状態だと言えるのはどれだろうか？そして結局何種類の準位が存在しているのだろうか？

この疑問に答えるためには角運動量の合成の話に立ち返らなくてはならない.p 軌道に入る電子はどれも全角運動量の量子数が l=1 であって,の違いはその向きの違いを表しているだけである.それで, l=1 どうしの角運動量の合成を思い出して計算してみる. 9 通りの状態しか出てこないし,これが先ほどの 15 通りの状態とどんな関係があるというのだろうか？その解決の前にこの 9 通りの状態について簡単に説明しておこう.原子内の個々の電子は様々な角運動量状態を取るわけだが,それぞれが角運動量をやり取りし合う結果として,保存するのは合成後の全角運動量だけであって,個々の状態は安定しないというか,あまり表立っては現れないような重ね合わせ状態として存在している.それを表しているのがこの 9 通りの式である.

今後は合成後の全角運動量の量子数を大文字ので表して,個々の電子の角運動量の量子数と区別しやすくしておこう.(1) ～ (9) 式の左辺は |L,M>} を意味しており,は全角運動量の成分を意味する量子数である.念の為にここでも言っておくが,は全角運動量の大きさを区別するための量子数なのであって,実際の全角運動量は ℏ√(L(L+1)) である.

例えば (1) ～ (5) 式の状態は全角運動量が L=2 であり,その方向によって 5 通りの状態が有り得る.つまり (1) ～ (5) 式は見ている向きによって軸方向の成分が異なっているだけであり,どれも大して違いのない状態なのである.同様に (6) ～ (8) 式の 3 通りの状態は全角運動量が L=1 でそれぞれに向きの違う,いわばどれも似たような状態である.同様に (9) 式は L=0 の状態である.

先ほど表にした 15 通りの状態は,実は安定して存在するわけではなく,それぞれの状態が量子力学的に重ね合わさった感じになっている.つまり全角運動量を保存するような (1) ～ (9) 式の形のいずれかに近い状態になって存在していることになる.

しかしなぜ 15 通りの自由度がないのかという疑問がまだ残っている.そのためにはスピンの合成もしてみないといけない.以前の記事でそれもやっているので結果をそのまま持ってこよう. これらの左辺は |S,S_z>} という形で表しているが,が全スピン角運動量の量子数, S_z はその軸成分を意味している.(10) ～ (12) 式は S=1 の状態で向きが違うだけの似た状態である.これらは「三重項状態」と呼ばれているのだった.そして (13) 式が S=0 の状態である.こちらは「一重項状態」と呼ばれている.

これらを使って今から軌道角運動量の状態を表す式とスピン角運動量を表す式とを合わせた状態を作ってみることにしよう.

まず (1) ～ (5) 式を眺めてみると,二つの電子の状態を入れ替えても全く形が変わらない対称的な形になっている.ところが電子というのはフェルミオンであり,二つの電子を入れ替えたときに位相が反転しなければならないという制約があるのだった.このままでは存在が許される状態にはなっていない.これを回避するためには,スピン状態を表す式の方で二つの電子を入れ替えたときに位相が変わるものを選んで合体させればいい.そういうわけで, (1) ～ (5) 式の状態に対してはスピン状態は (13) 式で表される形だけが一緒になることを許される.

ここで「位相が反転する」と言っているのは「波動関数の符号が逆転する」のと同じ意味である.複素数をイメージしているので位相が半回転するイメージの言葉遣いをしたくなるのである.

次に (6) ～ (8) 式だが,これは二つの電子を入れ替えると全体の符号が逆転するような形に既になっている.だからスピン状態の方は電子を入れ替えても符号が変わらない形で表されていないとこの性質を壊してしまう.つまり,(10) ～ (12) 式のいずれかが当てはまる.(6) ～ (8) 式の 3 つの状態のそれぞれに (10) ～ (12) 式の 3 つの状態のどれが付いてもいいのだから,9 通りの状態があることになる.

最後に (9) 式の状態だが,これは二つの電子を入れ替えても符号が変わらない形なので,スピン状態の方で符号が変わる必要性がある.つまり,(13) 式と一緒になる.

こうして,5 通り,9 通り,1 通りが得られ,全部合わせて 15 通りだ.自由度がちゃんと一致した.

LS結合という仮定

これで疑問は少しだけ解決したが,まだ大きな問題が残っている.結局,p 軌道に 2 つの電子が存在している状態というのは,何通りのエネルギー準位を作るのだろうか？

話を続けるために重要な仮定を導入しなければならない.それは「エネルギー準位は全軌道角運動量と全スピン角運動量との互いの向きの関係で決まるだろう」というものだ.このイメージを「LS結合」と呼ぶ.これがなぜ重要かと言うと,これは必ずしも正しいとは言えないかもしれないものだからだ.もし現実の現象の観察と合わないことが出てくるなら,この仮定を疑うべきなので覚えておいてほしい.

LS結合のことを別名「ラッセル-サンダーズ結合」と呼ぶが,LS はその二人の名前の頭文字ではない.綴りは Russell と Saunders である.

この仮定のイメージを説明しておこう.もし電子どうしの間に働く電気的な反発力が強ければ,それは電子が空間的な移動をするときに互いに強く影響を与え合うことになり,互いの軌道角運動量を頻繁にやり取りし合うことと等しい.つまり,個々の電子の軌道角運動量は保存せず,それらを合成した全体の軌道角運動量を保存するような状態だけが安定的に存在する.そしてそのやり取りから取り残されたスピンどうしが磁気的に影響を与え合って全体のスピン角運動量を保存するような状態を作る.いや,実際はスピンどうしのやり取りはほとんどないのかも知れないが,角運動量保存則がある限りは何らか形で全スピン角運動量を保存するだろう.ひょっとするとそれはそれぞれの原子ごとに終始ほぼ固定されたままかもしれないが,そこまではよくわからない.個々の電子のスピンと個々の電子の軌道角運動量の向きによるエネルギーはほとんど無視できるし,互いの角運動量のやり取りもないかもしれない.しかし全スピン角運動量に対する全軌道角運動量の向きについては無視できないほどのエネルギーの違いを生むことになる.あるいはそういうイメージでまとめて考えておけば,細かいやり取りの結果の全体とおおよそ一致するのではないか,という楽観論である.

実際このイメージは原子番号が 30 を超える辺りで成り立たなくなっていくそうだ.原子番号 30 番と言えば,だいたい M 殻を埋め切った辺りだ.おそらくは原子番号が大きくなると電子の軌道が外側に大きく広がっているので電気的な影響力をそれほど与え合わないようになり,軌道角運動量どうしで合成が行われるのではなく,個々の電子の「軌道角運動量とスピンの間」での磁気的なやり取りのほうが主流となり,それぞれの電子の（スピンをも含む）全角運動量どうしの配置によるエネルギー差を考えないといけないようになる.こちらのイメージを「jj結合」と呼ぶ.というのは軌道角運動量とスピン角運動量を合成した角運動量を表すのによく使われる記号である.

さて,jj結合を仮定して考えるのはいかにもややこしそうである.そのためか,LS結合を仮定してスペクトル項を考える流儀が広く使われている.その流儀で使われる項記号は「ラッセル・サンダーズ項記号」と呼ばれている.原子番号が大きくなるとこの仮定は成り立たなくなっていくと言っているのに,原子番号の大きな原子についてもこの流儀の項記号を当てはめたりすることが多いので不安になる.実際,現実と一致しない例も出てくる.

この記事でも,LS結合の話をする前から軌道角運動量だけ,スピン角運動量だけをそれぞれ合成する話をしてきた.それは最初からLS結合のイメージを仮定していたのである.角運動量の合成についていかにもそれが真実のように話してきたが,必ずしもそういう状態を取るとは限らないということだ.

どういう記号を使って分類すればいいか

結局のところ,我々がスペクトル項を分類するために必要な指標は 3 つだけである.全軌道角運動量と全スピン角運動量と,それらの向きの関係がどうなっているかを表すもう一つの何らかの指標である.この第 3 の指標としてはとを合成した角運動量を使うと便利である.

角運動量と角運動量という二つの量子力学的な量を合成したときにどんな結果になるかは我々は既に良く知っている.互いの向きによって様々な全角運動量を持つ状態が生まれることになるのだった.とが同じ向きを向いていれば J=L+S であり,全く逆方向を向いていれば打ち消し合って J=|L-S| となる.そしてこれらの他に最大値 L+S から最小値 |L-S| に至るまでの,値が 1 ずつ異なる幾つかの状態も生まれるが,それはそれぞれの角運動量が異なる向きを向いていた場合に相当するのである.このように,についてはとが分かっていれば全通りの状況を書き出すことが出来る.我々はの値にはそれほど関心はないのだが,ただ互いの向きの関係を区別するための指標としてそれを用いたいのである.

なぜの値そのものにあまり関心がないかと言うと,との相互作用のエネルギーを計算する際に要るのはとの積のような量であって,和ではないからである.

というわけで, (L,S,J) という 3 つの数値を並べてやれば目的は果たせる.しかし伝統的に別の記法を使うことになっている.

全軌道角運動量の値をわざわざアルファベットに置き換えて表すのである.方位量子数の l=0,1,2,3,… に対して s,p,d,f,g,h,i,… というアルファベットで軌道を表すのに倣って,に対してという大文字アルファベットを使う.そしてこのアルファベットの左上に 2S+1 という計算式に当てはめて出てくる値を書く.右下にはの値をそのまま書く.もしかのいずれかが 0 だったならばは一通りしか出てこないので区別する必要がなく,何も書かないことがある.なんとも一貫性のない面倒な記法だ.

例えば次のような見た目になる. 左上に書いてある数字が間接的に全スピン角運動量を意味している.この値が 1 なら S=0 で,2 なら S=1/2 で,3 なら S=1 で,4 なら S=3/2 といった具合である.ひょっとすると左上に分数を書くことを嫌ってこのような面倒な表記を選んだのかも知れない.スピンの合成なので電子数が奇数の場合にはスピンの上下をどう組み合わせたとしても必ず分数が現れることになるからだ. 2S+1 という計算式には一応物理的な意味があって,スピンだけを考えたときの状態の数を意味している.スペクトル項としては一つにまとめて表しているけれども,スピン状態としては 2S+1 個の状態がそこに重なって存在しているという意味である.これを「スピン多重度」と呼ぶ.

そういう意味では 2L+1 というものを考えてみても同じような意味がある.スペクトル項としては一つにまとまっているけれども,軌道角運動量だけを考えれば 2L+1 個の状態が重なっていると言えるわけだ.ならば,軌道角運動量とスピン角運動量の両方を合わせて考えると,その両者の組み合わせの数だけの個別の状態があることになりはしないだろうか？一つのスペクトル項には (2L+1)(2S+1) 個の状態が重なっていることになるわけだ.

実はこの推論は微妙に間違っている.この後でその間違いに自然に気付くことになるのでそこで説明し直すことにしよう.

やっと答えが出る

一つの例を説明するだけでここまで引っ張ってきてしまったが,やっと最初の問題に答えを出すことが出来る.p 軌道に電子が 2 個ある場合のスペクトル項は全部で幾つあってどう表せるのか.

(1) ～ (5) 式はどれも L=2 の同じ状態だと言えるものなのだった.そしてこれらにつながるスピン状態はどれも (13) 式で表せる状態,つまり S=0 の状態である.つまり, (L,S,J) は (2,0,2) となるから,項記号は次のようになる. (2・2+1)(2・0+1)=5 となるし,5 通りの状態が重なっている事がわかる.

次に (6) ～ (8) 式,これは L=1 の状態であり,これらにつながるスピン状態は (10) ～ (12) 式で S=1 である.このとを使ってを書き出してみると J=2,1,0 の 3 つがあるから,項記号は次のようになる. (2・1+1)(2・1+1)=9 となるので,9 通りの状態が重なっている事がわかる.あれ？おかしい.項記号は 3 つ出てきた.このどれもが共通する 9 つの状態の組み合わせで出来ているのだろうか？それとも 9 つの状態を 3 つずつ分け合っているのだろうか？

この疑問に答えるためには L=1 と S=1 を合成するときにどんなことが起きるかを考え直さなくてはならない.数学的には, l=1 と l=1 を合成して (1) ～ (9) 式を導いたのと同じことが起きている.つまり同じように, J=2 が 5 つの状態を作っており, J=1 が 3 つの状態を作っており, J=0 が 1 一通りの状態を作る.合計で 9 通りである.これらの状態は結構面倒な重ね合わせで作られているものであり,(6) ～ (8) 式の中のどの状態がどのに属しているかという具合には分けられない.

先ほど説明した幾つかの点を訂正しておこう.

まず,「の値にはそれほど関心はない」と言ったことを撤回する必要がある.それぞれのスペクトル項に (2J+1) 通りの状態が存在しているという重要な情報が読み取れる.

そして「一つのスペクトル項には (2L+1)(2S+1) 個の状態が重なっている」と言ったことも間違いだ.との両方が共通しているスペクトル項を全て集めて考えれば個の状態から出来ている,と言うべきだった.

さて,元の話に戻ろう.残るは (9) 式である.これは L=0 であり,(13) 式の S=0 とつながるのだった.だから J=0 であり,項記号は次のようになる. 長い話だったが,結局は p 軌道の 2 つの電子は 5 つのスペクトル項を生じるのだというのが結論である.

他の幾つかの例

一つの例を説明するだけでこんなに長くなってしまった.さぞ気が遠くなっていることだろう.私はもうふらふらである.

p 軌道に電子が 2 つというかなり単純な例を考えたからこれだけで済んだのだが,これが d 軌道,f 軌道だったり,電子数が 3 つ,4 つ,5 つだったらどうしたらいいだろうか？電子の配置パターンはとてつもなく増えてしまうだろうし,3 つ以上の角運動量の合成を考えるのはかなり面倒になる.

3 つの電子の角運動量の合成をしようと思ったら 3 つの下降演算子の和を作って順々に作用させていけばいいのだが,直交化しようとする辺りで自由度が有りすぎて少し(いや,かなり？)嫌になるだろう.3 つ以上を一気に合成するのではなく,まず 2 つの角運動量を合成した結果を使ってさらにそこに一つずつ合成していくという考え方もあるし,行列を使ったりして計算手順を機械化して思考の迷いを軽減するという方法もあるが,どちらにしても面倒である.しかも軌道角運動量を合成したものとスピン角運動量を合成したものを組み合わせようとするときには,どの電子を入れ替えても符号が変わるようなパターンを見つけ出さないといけない.

気分転換に,s 軌道に電子が 1 個だけある場合を考えてみよう.面倒な計算は必要ない.軌道角運動量は L=0 であり,スピンは上向きと下向きのどちらも有り得るが,全スピン角運動量はスピンの大きさだけが問題なのであり, S=1/2 である.このとから J=1/2 しかないことが分かる.項記号は次のようになる. とても簡単に済んでしまった.調子に乗ってもう一つやってみよう.s 軌道に電子が 2 個の場合はどうだろうか？これは s 軌道を完全に埋めているので励起状態としてはこれらの電子の一方,あるいは両方が,さらに上の p 軌道あたりに飛び出して行った後のことを考える必要があるが,それはまた別に計算してやればいいのである.ここでは s 軌道だけのことを考える.とは言っても s 軌道はもう満杯なのだから状態は一通りしかないし,こんな状態について考えようとする動機そのものが不明だ.強いて挙げるなら,あらゆる状況を共通の手続きで記号化しておいてやりたいと言ったところである.

軌道角運動量については計算するまでもなく L=0 である. l=0 であるものを二つ合わせても 0 だからだ.一方,スピンはといえば上向きと下向きが合わさって S=0 だと即答してもいいのだが,もう少し丁寧に考えてみよう.これは s=1/2 どうしの合成であり,(10) ～ (13) 式と同じ 4 つの状態が得られる.軌道角運動量の方は |0>}|0>} と表される状態になっていて電子の入れ替えをしても符号が変わらないのだから,スピン状態の方で符号が変わるものを選ぶ必要がある.それは (13) 式のような状態だけであり,必然的に S=0 なのだと理詰めで断言できることになる. L=0 で S=0 なら J=0 しかないので項記号は次のようになる. p 軌道に電子が 1 つきり,という状況も考えておこう.合成を考える必要もないから簡単すぎて楽しい.この軌道は l=1 であってこれだけしかないのだから L=1 である.スピンも合成する必要がなく S=1/2 である.を求めてやると,3/2 と 1/2 の 2 つが現れる. 軌道角運動量とスピン角運動量が同じ方を向いているか逆方向かによって二つのエネルギー準位が生じるのだろう.

予定外だが,さらにもう一つ考えてみよう.p 軌道に 6 個の電子がある場合,つまり,軌道を全て埋めている場合だ.6 個の電子の合成をわざわざ考えるのは面倒だが,状態の自由度は唯一つしかないのだし,全ての磁気量子数は打ち消し合うような入り方をしているのだから L=0 であろう.つまりまともにやれば (1) ～ (9) 式のような形よりもずっとずっと複雑な状態がそれこそ多量に出てくるが,許される状態の自由度が唯一つしかないことは分かっているのだから,その多量の式の中の L=0 となるようなものだけが生き残るに違いない. L=1 なら 3 通りの状態が出てきてしまうだろうとか, L=2 なら 5 通りの式が出てきてしまうだろうとか,そういう理屈である.スピンについても同様で S=0 である.そういうわけで,項記号は s 軌道にいっぱいまで入っているときと同じ, という記号で表されることになる.このように,項記号が同じならば同じエネルギー準位だということでもないのだ.ある原子で生じる幾つかの励起状態を区別するためだけのものだと理解してもらいたい.

簡単に探す方法

さて,簡単に導けるような例はほとんどやってしまった.しかし手が付けられない状況の方がはるかに多く残っている.ここまでこんなに長く説明してきたというのに,この成果の少なさは絶望的だ.

何とか最終結果だけを導く近道のような手順はないものだろうか？いちいち具体的な状態の式を求めることは今の私としては放棄しても構わないのだ.ここまでやってきたことの中からヒントを見つけ出してやろう.

最終的にはとさえ求めてやればが全て求まるのである.の最大値が幾つになるかを知ることは簡単だし,の最大値が幾つになるかを知ることも簡単だ.それらの値を 1 ずつ減らして 0 または 1/2 に至る全ての状態が存在していることも,角運動量の合成の理論から分かっている.最大の難関は,が幾つのときにが幾つのものをペアにすれば存在が許されるかという組み合わせを知ることだ.

ヒントはまだ他にもある.最初に全ての実現しうる電子配置の表を作ってみたのだった.現実の現象としてはそれらの状態が複雑に重ね合わさった状態を取るのでそのイメージは間違いなのだが,それらを組み合わせたもので出来ているからには互いに独立な状態の全体数は変化しないのである.さらには,を求める前のとだけが決定した状態については, (2L+1)(2S+1) 個の状態が含まれるのだった.このような数字パズル的な方法で,全部の辻褄が合う状態を一通りに定めることが出来るのではないだろうか？

最初に作った表というのは電子が同一の状態を選ばないようにするという条件を満たすように作られている.この「パウリの排他律」というのは,電子を入れ替えたときに位相が逆転するという条件と等価である.それについては第 5 部の「ボソンとフェルミオン」という記事で説明しておいた.つまり,あの表に含まれている軌道角運動量とスピン角運動量の組み合わせは,電子のフェルミオンとしての性質を既に反映させたものになっており,許されない状態は省かれているのである.

よし,最初に作った表をもう少し拡張して情報をもっと抜き出してみることにしよう.すべての状態に対して,磁気量子数の合計値とスピン量子数の合計値を計算してみる.

	m=1		m=0		m=-1		m の合計	s の合計
[1]	↑	↓					2	0
[2]	↑		↑				1	1
[3]	↑			↓			1	0
[4]	↑				↑		0	1
[5]	↑					↓	0	0
[6]		↓	↑				1	0
[7]		↓		↓			1	-1
[8]		↓			↑		0	0
[9]		↓				↓	0	-1
[10]			↑	↓			0	0
[11]			↑		↑		-1	1
[12]			↑			↓	-1	0
[13]				↓	↑		-1	0
[14]				↓		↓	-1	-1
[15]					↑	↓	-2	0

そして,このの合計値との合計値の組み合わせを 2 次元上にプロットしてみる.

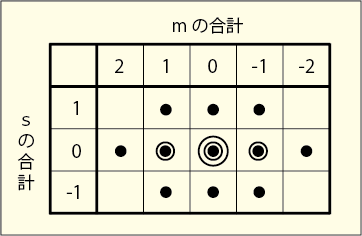
重複するところは二重丸,三重丸にしておいた.もっと電子数が多い場合には記号が足りなくなるので数字にしてもいいし,正の字を書きながらカウントしてもいいだろう.

この図を見ながら考えるに,横並びの 5 つの点は L=2 の 5 つの状態を表しているが S=0 に限られている.中央の 9 つの点は L=1 を構成する 3 つと S=1 を構成する 3 つが組み合わさっているのだろう.残りは中央の一点で L=0 かつ S=0 を意味している.つまり次のように分解して考えることが出来るわけだ.

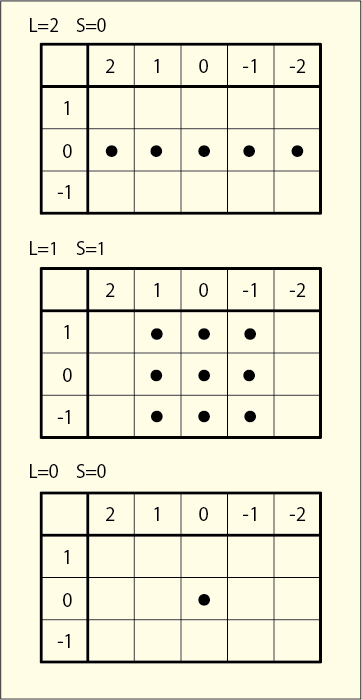
これらの点は必ず長方形状に配置することになるということをヒントにすれば分解しやすい.一つ一つの点は自由度を表しているので (2L+1)(2S+1) という並びを構成するはずなのである.

この手法はこれまでの話を元にした数値合わせパズルのようなものなので,これを元にして実際の現象を把握しようとしても的外れな解釈に陥ってしまうだろう.電子が実際はどんな状態になっているのかは実に把握しにくい.とがそれぞれに保存するというイメージまでならこの簡易手法がある程度の状況を示してくれているが,さらにとの相互作用によってエネルギー準位が分かれた状況までを考えると,それらの状態がさらに組み合わさった状態になっているとも解釈できるのである.見る方向や観測方法によってそれぞれ違った状態に分解して考えることができるという,量子力学ではお馴染みの状況である.