電磁場の熱平衡
物質が熱放射を行っていることはかなり前から知られていたが,その正体が電磁波であることは電磁気学が完成に近付いてようやく明らかになったのである.
もし物質が熱放射を行う一方だとすると,どんどんエネルギーを失って冷えてしまうだろう.いや,実際そういうことはあるのだ.天気予報などで「放射冷却現象」というのを時々聞くことがあるだろう.良く晴れて雲一つない日には,地表からの熱放射が何にも遮られることなく宇宙空間へ向けてどんどん逃げてしまうため,気温が急激に下がったりする.
しかし断熱容器の中に置いた物体の温度が勝手にどんどん下がってしまうことはない.全てのエネルギーが電磁場に渡されるなんてことはなくて,およそ一定の温度に落ち着くのである.これは電磁場と物質の間に一方的でない熱のやり取りがあって,やがて熱平衡と呼べる状態に達するからであろう.すると,電磁場にも温度というものがあるに違いない.
まぁここまでは前回も話したし,電磁場の温度とエネルギー密度の関係を導き出すこともやったのだった.しかし,まだ疑問はある.
熱平衡に達した電磁場には色んな周波数の電磁波が含まれているに違いない.一体,どんな周波数成分がどの程度ずつ混じっているのだろう.別の言葉で言えば,電磁波の「スペクトル分布」がどうなっているかということだ.
ところで,このスペクトルというのはもともと,光をプリズムで七色に分解した時の美しい模様のことを指す言葉だった.可視光線は電磁波の一種であり,その周波数によって色が違う.つまり,このプリズムの七色模様は電磁波を周波数ごとの成分に分解して見ているのである.やがて可視光線以外の電磁波についても周波数ごとの分布の具合のことをスペクトル分布と呼ぶようになった.
今ではこの言葉は電磁波以外にも使われており,例えば,音を周波数ごとに分解してその強さの分布を表示したものもスペクトル分布と呼ぶようになっている.
熱平衡というのは安定に達した状態なのだから,時間の経過によってスペクトル分布が次々に変化するということはないであろう.物質によって吸収しやすい周波数というものがあるだろうから,もしスペクトル分布が時間とともに次々と変化するようであれば,物質の温度もそれに合わせて変化してしまうはずだ.そんな現象は起きていない.よって,それは気体の速度分布と同じように一定の分布に落ち着いているのではないかと考えられる.
だがしかし,その分布は果たして温度だけで決まるとまで言えるのだろうか?電磁波を放射する仕組みは物質によって色々あるだろうから,物質によってはある特定の周波数の電磁波を強く放射していたりもするだろう.どんな材質の物体と熱平衡に達しているかによって,そのスペクトル分布は異なっているのではないだろうか.
ところが,その考えは否定されるのである.
熱平衡のスペクトルは温度だけで決まる
例えば 2 つの密閉容器があって,それぞれの壁の材質は違っているとする.しかしどちらの壁も同じ温度になっており,その内部の電磁場との間で熱平衡に達しているとする.ここで,両方の容器の壁に小さな穴を開けてやって,お互いの内部の電磁波が行き来できるようにしてやるとしたら,一体何が起こるだろう.
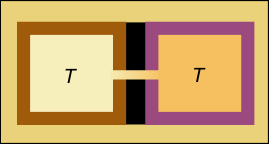
もしそれぞれの容器内の周波数成分の割合が違っているとすると,他方に比べて少なかった成分が流入してくるだろうし,逆に流出することも起こるだろう.しかし材質によって,どの周波数成分の電磁波を効果的に吸収できるかという特性には違いがあるはずだ.その新しく入ってきた周波数成分を吸収する度合いはそれぞれの壁で差があるので,一方の壁の温度は上がり,他方は下がるなどということが起こり得る.
一度は同じ温度になったもの同士を接するだけで勝手に温度差が生じるという,熱力学の第 2 法則を破る事態が生じるわけだが,果たしてこれは本当だろうか?これを利用すれば永久機関を作ることが可能になるはずだ.
この段階ではそれを否定する根拠は乏しいのだが,ここでは仮に,そんなことは実現し得ないのだとしておこう.要するに,壁がどんな材質で出来ていようとも,熱平衡にある電磁場のスペクトル分布は皆同じで,温度だけで決まってしまうのだ,という結論を受け入れようということだ.
だとすると次に,なぜそんな不思議なことになっているのかを考える必要がある.
キルヒホッフの法則
熱平衡にある電磁場のスペクトル分布の形をという関数で表しておこう.この分布は温度によって形が変わるだろうから,変数に
も含めて
と書いておいた方がいいだろう.これは,周波数が
の範囲にある電磁波のエネルギー密度が
であるという意味でもある.
壁が電磁波をどの程度吸収するか,という度合いもやはり周波数によって違うだろう.それは壁の材質によっても違うだろうし,壁の温度によっても違うかも知れない.それで吸収率をと表そう.
もう一つ.壁がどの温度のときにどれだけの放射を行うかを表す関数も用意したい.これも材質によって色々な形があるだろうから,と表すとしよう.
これらの関数を使うと,熱平衡にあるときに,の範囲にある電磁波から壁が吸収するエネルギーは次のように表される.
一方,熱平衡というからには同じ量のエネルギーを,同じ周波数で常に放出していなくてはならないから,次のような等式が成り立つはずだ.
これは,吸収したエネルギーをすぐさまそっくりそのまま反射するという意味ではない.ある周波数の電磁波から受け取ったエネルギーを,別の周波数の電磁波に変えて放出しているかも知れないだろう.この議論は原子の内部構造がまだほとんど分かっていなかった頃に行われたものであって,放射の詳しい機構にまで踏み込んではいないことに気をつけよう.とにかく,熱平衡であるからには,このようなバランスが成り立っていなくてはならないのは確かなのだ.
この式を変形すると次のようになる.
この式は何を意味しているだろうか.右辺にある関数はどちらも材質に依存するのに,左辺は材質に無関係になっているのである.これは,ある周波数の電磁波を吸収しやすい材質は,同じ周波数の電磁波を放出しやすい材質でもあるということだ.これが熱平衡時に材質に関係なく同じスペクトルが実現する秘密である.物質が電磁波を放出する機構と吸収する機構は共通しているということを暗示しているようでもある.
こういうことをあれこれと考えていち早く発表したのはキルヒホッフであった.電気回路の計算に必ず出てくるあの「キルヒホッフの法則」で有名なキルヒホッフである.それで,この式も「キルヒホッフの法則」と呼ばれている.
黒体放射
ここで,あらゆる周波数の電磁波を完全に吸収するような物質があったらどうなるか,ということを考えてみる.それは常温では真っ黒に見えるはずである.そういうわけでそのような仮想的な物質を「黒体」と呼ぶことにしよう.それは周波数に関係なく常にであるということだから,キルヒホッフの法則に当てはめると,
となるであろう.
というのは熱平衡にあるかどうかに関係なく物質が放射するエネルギーを表しているのだった.だからそのような完全吸収体があるとしたら,それは熱平衡にない場合にも,常に熱平衡のときと同じスペクトルの電磁波を放射するという性質を持つであろう.黒体から放射される電磁波を「黒体放射」と呼ぶ.黒体放射は熱平衡にある電磁場と同じスペクトルを持つということである.
問題はそんな物質が実際にあるかということだ.見た目が黒いというだけでは条件を満たさない.しかし例えば,プラチナブラックとか白金黒(はっきんこく)とか呼ばれる物質は黒体に割りと近い性質を持つと言われている.これはプラチナの微粉末で,真っ黒な物質である.あるいは白金の表面に白金をメッキするとこれと似た状態になる.他には木炭やグラファイトの粉末なども黒体の例として挙げられることがある.
しかし,もしそれら現実の物質の放射スペクトルと,後に理論的に導かれる黒体のスペクトルとを比較したグラフを見る機会があるとしたら,こんなにも違うものなのか,と驚くかも知れない.全周波数にわたって電磁波を完全に吸収するというのは難しく,グラフの所々がギザギザになっていたりする.そもそも完全な黒体があったとしたら,そこだけ空間にぽっかり黒い穴が開いたように見えるはずなのだ.それでも普通の物質と比べれば,はるかに黒体に近いとは言える.
 | 近頃はそういうびっくりするほど真っ黒な塗料も市販されるようになった。 とは言っても、これは可視光の範囲だけだろう。 模型用なのでエアブラシなどによる塗装が必要だし、塗装後に触ると効果が消えてしまうようである。 |
空洞放射
黒体というのは理論上の存在である.現実に存在しないのならば,あまりその性質について興味を持てないかも知れない.しかし黒体放射に非常に近いものを人工的に作り出して現実に測定することは可能なのだ.
その為にはこうすればいい.次の図のように,物体の内部に空洞を作ってやり,狭い穴を作ってやる.材質は不透明でありさえすれば何だって構わない.内壁にはツヤがない方がいい.
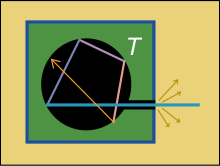
その穴から内部に飛び込んだ光は中で乱反射するだろう.そして外に出るチャンスを得る前にそのほとんどが内部の壁に吸収されてしまう.これは黒体と非常に良く似た状況だと言えるだろう.実際,この穴をのぞくと中は真っ暗だ.しかしこの穴からは,内部の壁の温度に応じたスペクトルを持つ電磁波が出てくる.これを「空洞放射」と呼び,黒体放射とほぼ同じ意味の用語として使われる.
実際に測定してみると,それは材質によらないスペクトルになっており,キルヒホッフの考えは正しかったようだ.そして永久機関を作れる可能性も無事に否定されたことになる.
しかし空洞放射のスペクトル分布の形が一体どんな式で表されるのか,それはどういう仕組みによるのかについてはまだ何も説明できてはいない.そのための理論を考えることが必要だ.次回からはそういう話に入ることにしよう.
ところで,先ほど紹介した白金や炭の微粉末が黒体に近い性質を持つのは,その物質固有の性質というわけではなく,主にその表面の形状に由来しているようである.その粒の径が非常に細かかったり,表面に無数の穴が空いているために,今説明した空洞と同じような多数の微細な構造が自然に出来上がっているせいだろうと考えられる.
ステファンの実験が認められなかった理由
前回,ステファンの実験を確認するための実験がうまく行かなかったということを話したが,今回の話を考慮に入れればその理由が見えてくるだろう.理論的にはボルツマンの説明は正しかったのだ.しかし実験において注意すべき幾つかの考えが抜けていたのだった.
ある周波数の電磁波の放射と吸収の度合いは材質によって違うのである.発熱体からの放射を,受ける側は完全に吸収できるわけではないということだ.しかも温度によって放射と吸収のスペクトルがそれぞれの物体で変わるのだから,受け側に黒体でも使わない限り,めちゃくちゃな測定結果が出ることになるだろう.
そしてもう一つ.ボルツマンの理論的説明には電磁場が「熱平衡」にあることが暗に含まれていたのだった.電磁場の温度というのは熱平衡において,ようやく決まるものなのだ.ステファン・ボルツマンの法則を適用するのに大切な条件というのはそのことである.しかし熱平衡でなくても良い場合がある.黒体からの放射ならば,その電磁波は熱平衡と同じ状態にあると言えるだろう.発熱体が黒体に近い性質を持っている場合には,ステファン・ボルツマンの理論に近い放射が得られるということだ.
キルヒホッフの理論の方が 20 年近くも前に発表 (1859 - 1860) されていたにも関わらず,この頃はこのことの重要性がまだ十分に理解されてはいなかったのである.










