熱放射の研究の背景
19 世紀末のヨーロッパでは帝国主義的な傾向が強まり,国々の間で軍拡競争が始まった.特にドイツの資本主義の発展はめざましかった.1871 年,普仏戦争の勝利によってドイツはフランスから莫大な賠償金と,良質な石炭と鉄鉱石を産出するアルザス・ロレーヌ地方を手に入れ,鉄鋼の生産はイギリスを凌ぐほどになりつつあった.
品質の良い鉄鋼を生産するためには,さまざまな工程における厳しい温度管理が欠かせない.高温の炉の温度を素早く正確に計測する技術の開発が急務であった.そこで注目されたのが空洞放射である.炉から出る光の色を利用して,溶けた鉄の温度を瞬時に知ろうというわけだ.
最終的にはその試みはうまく行った.「光高温計(ひかりこうおんけい)」というものが発明されたのである.その原理は簡単で,炉から出る光を背景にして,電球のフィラメントに電流を流して発光させ,背景とフィラメントが同じ色になったときの電流計の目盛りを読むことで温度を測るのである.しかし実用化のためには熱放射についての色々な性質を正しく知っている必要があった.
こういう背景があって,熱放射の研究は単なる科学的興味だけではなく,国家的事業の要求にも後押しされて進められることになったのである.
ウィーンの変位則
当時から見れば遥かな未来に生きている我々の特権として,正確な空洞放射のスペクトルの全体像を先に見てしまうことにしよう.しかしその数式はまだ明らかにしないままにしておく.
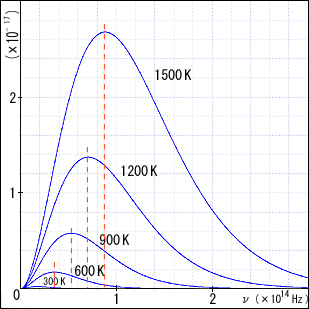
ちなみにこのグラフは赤外線の領域であり,可視光線はこのグラフの横軸の 4.1 ~ 7.9 くらい,それ以上が紫外線の領域になる.
このグラフから何が読み取れるだろうか?まず,温度が高くなるほど,放射の強度が急激に上がることが分かる.これはステファン・ボルツマンの法則からも分かることであり,全周波数成分の合計,すなわちこのグラフを積分した面積はに比例するのである.
その他に,温度が高くなるほどグラフのピークが右側へ移動しているのが分かる.温度によって炉から出る光の色が変わって見えるのはこのためだ.実は,ピークの周波数と温度には正比例の関係があり,これを「ウィーンの変位則」と呼ぶ.これは 1888 - 1890 年頃に発表された様々な実験報告から明らかになったことだが,その数年後,1893 年になってウィーンが理論的に導くことに成功したため,こう呼ばれるようになったのである.
以前に,太陽の表面温度が約 6000 ℃であることを裏付ける別の方法があると書いたが,この法則のことを言っていたのである.太陽光線のスペクトル分布を調べて,そのピークの周波数が幾つであるかを調べればいい.しかしこれよりさらに素晴らしい応用もできるようになった.遠くの恒星が放つ光のスペクトルを測定することで,その表面温度を推定することもできるのである.これによって天文学は飛躍的に進歩することになった.
ところで,ウィーンの変位則は当時,どのようにして証明されたのだろうか?現代の視点からならばそれを導くのは簡単だ.スペクトルの形を正しく表す公式がすでに知られているので,それを微分して 0 になるところがグラフのピークだと考えれば求められるだろう.今はそのように説明してある教科書ばかりである.
しかし当時の知識だけから一体どうやってこれを導くことが出来たのかを知りたいのだ.それは実に巧妙な方法であった.
理論的導出
これから,空想的な実験を考えてみる.これを現実の世界で試してみるのは色々な意味で難しいだろう.思考実験というやつだ.思考過程に合わせて次々と設定を変えるので,気を付けてついてきて欲しい.
まず,内部が真空の断熱容器を考える.その温度はだとする.するとこの内部は真空だとは言っても,電磁波だけは存在するわけだ.電磁波に圧力があることは少し前にも話した.ステファン・ボルツマンの法則はそれを応用して証明したのであった.
この容器にはピストンが付いているとする.これを押し込もうとすると,電磁波の圧力に抗するわけだから,エネルギーが要る.断熱過程なので,そのエネルギーの全ては,内部エネルギー
の増加に使われることになるだろう.ところで,そのときの内部エネルギー密度
の増加はどれくらいになるだろうか?たとえエネルギーの増加がなかったとしても,体積が減ればその分だけエネルギー密度は増す.だから,今回はエネルギーの増加と体積の減少との二つの効果が重なるわけだ.計算してみよう.
圧力で微小な体積変化
をさせるときの内部エネルギーの変化は,
である.一方,内部エネルギー
と内部エネルギー密度
の間には
の関係があるので,
という関係も言える.これらの式を合わせれば,
という関係があることが導ける.ところで内部エネルギーと温度の間には,ステファンボルツマンの法則
が成り立っているのだから,これを (1) 式に当てはめて,
という関係になっていると言えそうだ.
しかし,ここまでの話に問題はないだろうか?体積を小さくすると温度が上がるとは言っても,壁の温度を一緒に上げることまでは考えていない.ここでのというのは電磁波の温度のことだ.壁の温度まで一緒に上げることを考えると,ほとんどのエネルギーはそちらに食われてしまうだろうし,壁の厚みや材質などによって話が変わってしまう.だから,もはや壁の存在なんかは無視したいのである.容器の内壁が鏡のような完全反射体になっていて,しかも外部の熱を完全に遮断しているという特殊素材を想定したら良いだろうか.
それでも困るのだ.一体,壁と熱平衡にない状態での電磁波の温度とは何だろう.ピストンを押せば確かに内部エネルギー密度は上がるだろう.しかしその数値だけを頼りに温度を決定して良いものだろうか.ここで前回の話を思い出してみよう.たとえ壁がなくとも,その電磁波のスペクトル分布が,ある温度の黒体放射と同じになっていたならば,それを電磁波の温度だとみなすことに反論はないであろう.問題は,今回のようにピストンを押したとき,内部の電磁波のスペクトル分布にどんな変化が起こっているのかということだ.熱をやり取りする壁がないものとして考えている以上,スペクトルが黒体放射と同じになるという保障などないではないか.
そこで次に,ピストンを押したときに,内部の電磁波にどんな変化が起こるのかを考えてみる.ゆっくりとした一定速度でピストンを押し込むとしよう.この移動する壁に当たって反射する電磁波は,ドップラー効果で周波数が上がるはずだ.それはどれくらい上がるのか,計算してみよう.
ドップラー効果は,観測者が移動する場合と音源が移動する場合の二通りあるのだった.今回はその両方である.電磁波のドップラー効果は厳密には音の場合とは違うのだが,今は相対論的な効果を考慮に入れる必要はないだろう.移動する壁にとって,元の周波数は
に変化したように感じられ,その変化した周波数で反射する.そして今度はその壁が移動発信源となり,静止している側から見れば
に変化したように感じられる.両方を合わせれば,結局,
であるから,周波数変化は,
と表せるというわけだ.
さて,しかし今回の場合,移動する壁に対して正面からまっすぐにぶつかってくる電磁波ばかりではないだろう.それこそあらゆる角度からぶつかってくるのである.それで例えば,壁に対して角度の向きで進む電磁波を考えてみる.
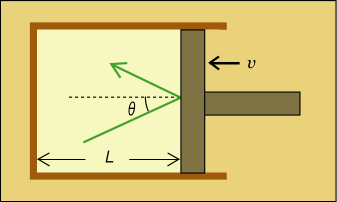
壁は,この進路に対して斜め横から迫ってくる形になるのであり,実際の速度よりも素早く進路を横切ることになるだろう.だから先ほどの式の
の代わりに,
を使ってやる必要がある.次に,この電磁波が再びこの壁にぶつかる頻度を考えよう.電磁波の横方向の速度成分は
であるから,長さ
を往復して戻って来るのに
秒だけかかることになる.つまり 1 秒あたりに
回の衝突をするのであり,その度に
の周波数変化があるのだから,微小時間
では
という変化が起こると言える.この結果に
が入ってこないということは,どの方向を向いた電磁波であろうと関係なく,一定時間に同じだけの周波数変化を受けるということを表している.これは考察がしやすくて助かることだ.ところでこの右辺にある
というのは容器の横方向の長さの縮み変化
のことであるから,この式は次のように変形できる.
上の図のような装置の構成の場合,容器の体積
と
とは比例するので,
が成り立つと考えたくなるし,それは間違いではないのだが,このやり方には一つの大きな問題がある.ピストンを押し始める前の電磁波は均等にあらゆる方向を向いていると考えていた.ところが一方向だけから押すこのやり方では電磁波の方向の分布に偏りができてしまうのである.それを解決するには容器の形を保ったまま,全体を均等に押し縮めてやる必要がある.最も考えやすいのは,一辺の長さが
である立方体を 3 方向から同じように押し縮めてやることである.そう考えた場合の体積変化は,各方向に順番に同じだけ少しずつ押し縮めたのと同じことなので,
と表せる.これを (3) 式に当てはめれば,
という関係があることが分かる.これと (2) 式の
を一緒にすれば,
と
とが比例関係にあることが結論できるのである.
これで数式的には変位則が導けたのではないだろうか.容器の中の電磁波には色んな周波数成分が含まれるけれど,それぞれの成分がそれぞれの周波数へと温度に比例して一斉にスライドするというイメージなわけだ.これが「変位則」という名で呼ばれる所以である.このことから,元々ピークであった強い周波数成分は,温度が変化した後でもやはり同じようにピークを維持することになるのである.
ん?・・・いや,そんなことが本当に言えるものだろうか.それぞれの周波数成分は周波数の変位を起こすだけでなく,同時にエネルギー密度も増加するのである.それぞれのエネルギー密度がどれも同じ割合で増加するというのなら,この話にもうなずけるだろう.しかし,もし元々のピークに近いところにある別の周波数成分のエネルギー密度が,ピークにあった成分のそれよりも少しでも多めに増加するようなことがあれば,ピークの地位はそちらに奪われるかもしれないではないか.
それに,周波数がスライドした結果,スペクトル分布も元の形から崩れるだろうが,その形は,その温度における黒体放射のスペクトルと同じ形だと言えるものだろうか.まだもう少しあれこれと考察が必要なようだ.
さらなる考察
我々の本当の目的は,スペクトル分布を表す関数の形を知ることである.エネルギー密度
というのは,これを全周波数に渡って合計したものであるから,次のような関係にある.
今,電磁波の温度が
から
へと変化し,それに合わせて
の範囲にある電磁波が,
へとスライドしたとしよう.この変化後のエネルギー密度は,同じ関数
を使って
のように表されると期待したい.本当は先ほどの思考実験からは同じ形の分布が実現することまでは言えないのだが,今は何としてでも
の形を推理したいので,このような仮定を置いて考えてみるより他ないのである.
さて,と
の間には,ステファン・ボルツマンの法則によって,
という関係があるであろう.だから,
という等式が成り立つところまでは言える.しかしこれ以上進むのは難しい.この積分記号を取っ払ってしまうわけには行かないからだ.しかし,もしステファン・ボルツマンの法則が各周波数成分ごとに成り立っていると仮定するならば,積分記号を外して両辺を比較できるだろう.この仮定は,現代の視点から見れば結局は正解だったのだ.しかしこの当時としては強い理論的根拠はない.とは言うものの,もしこの仮定が正しければウィーンの変位則が説明できるわけだから,間接的だが実験的な根拠は既にあるわけだ.
そもそもウィーンは,変位側が成り立っている理由を既知の法則だけから説明することを目的としていたのではなく,この法則が成り立つ根底にどんな未知の事柄が隠されているかを探っていたのだろうから,こういう思考方法も的外れとは言えないだろう.さて,積分記号を外すと,こうなる.
と
の関係は,既に導いた (5) 式の関係によって,
であると言えるし,同様に
であることも言えるから次のように整理できる.
さあ,この条件から,
がどんな形の関数であるべきか,類推せよ!
それをすぐに言い当てるのは簡単ではないが,この中には幾つかのヒントが見え隠れしている.は右辺にだけあって左辺にはないのだから,任意の定数のようなものだと考えてとりあえずは無視してやれば良いだろう.この数値が幾つであろうとも成り立っていなくてはならないのだから,1 とでも置いてやれば分かりやすくなる.そして,両辺ともに関数
が含まれてはいるのだが,その形は未知だ.右辺でだけ,
がその関数の外に飛び出している.左辺を見る限り
と
の関数であり,右辺も同じはずなのだが,この
を除外すれば,それは
にのみ依存する形の未知関数である.要するにこれは,
という形になっているだろうと言えるし,先ほどの条件に代入してやれば,確かにこれで良いことが分かる.しかしこれが唯一の形というわけではない.次のように変形することも可能である.
他の形にも書けるのだが,正解を知っている現代人の視点からすれば,次のように表現しておくのが一番分かりやすいだろう.
要するに,この形こそが,ウィーンの変位則に従いつつ,しかも積分するとちゃんとステファン・ボルツマンの法則を再現するような分布式の満たすべき条件だということだ.しかし残念ながら,これは十分条件だとは言えない.それについては次回に幾つかの失敗例を紹介しよう.
ウィーンの放射法則
ウィーンはここまでに得た幾つかのヒントと,あてずっぽうの独自の理論から,
という式を提案した.これを「ウィーンの放射法則」と呼ぶ.これは実に惜しい形をしているのだが本当の答えはまだ内緒にしておこう.どうやってこの式を導いたのか,という彼の説明は,今となっては大した価値はない.空洞放射の源は加熱された気体分子であり,そのスペクトル分布は分子の速度分布に依存しているだろうとかいう,現在では否定されている考えを基にして,飛躍した論理で議論しているからだ.
これを先ほどのグラフと重ね合わせてみよう.
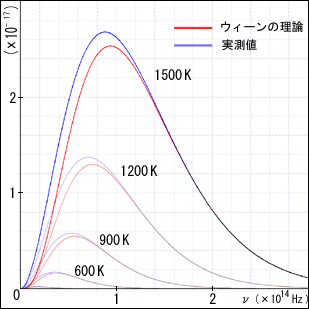
周波数の高いところではかなり一致することが分かる.まぁ,そうなるように合わせ込んで数式を作ったのであろう.すでに得られている実験結果と異なる式をわざわざ発表するはずもないだろうから.しかし周波数の低いところでは外れていることも分かる.実はこの当時,周波数の低い方の実験はまだ難しく,十分なデータが得られていなかったのである.それで,新たな実験結果が発表されるまでのしばらくの間は彼の理論は有望視されていたのだった.
隠れている真理
ところで,ウィーンはその意味と重要性に気付くことが出来なかったようだが,ここまでの議論の中に,将来明らかになる重要な真理がすでに顔をのぞかせているのである.
まず,(1) 式を見ると,となっている.全エネルギーは
だから,この式は,
という意味でもある.これと,(4) 式の
とを合わせてみれば,全エネルギー
と周波数
には比例関係があることが分かるだろう.体積変化に応じて,全ての周波数の電磁波が一斉に同じ比率で変化するのだから,これは容器内の全ての電磁波について同じように成り立つ関係であると言える.
これは古典的な電磁気学の範囲では説明できない関係である.実は,もう少し後に出てくることになる量子論のという関係を暗示しているのである.











元の数式はもっと難解ではある。