統計力学：古典統計との違い

歴史

第 3 部に入って「量子統計」というテーマで話を進めてきたわけだが,今までのところ特に新しい考えを取り入れた様子もなく,第 2 部で説明したのと同じ手法を当てはめることで幾つかの現象が説明できている.

いや,実は新しい考え方は入って来てはいるのだが,意識しないくらい自然にやったのである.理論を使いこなすためにはその点を意識の上に持ってきて,自在に使い分けることが必要であろう.しかし当時の科学者たちでさえ,ボースが指摘するまではあまり意識してはいなかったのである.

1924 年,インドのボースはアインシュタインに手紙を書き,自身の論文の内容を評価してくれるように頼んだ.その重要性に気付いたアインシュタインはそれをドイツ語で出版する助けをし,自らもその研究を進め,翌年,「ボース・アインシュタイン凝縮」という現象が存在することを予言するに至るのである.その現象については後ほど別の記事で説明しよう.

ボースの論文の内容は,簡単に言えば,こうである.つまり,光の量子というものについて,それらが互いに識別できない粒子であると考えるような統計を考えれば,そこからプランクの放射法則を導くこともできる,という証明であった.そしてアインシュタインは,そのアイデアは光だけでなく普通の物質粒子にも応用できるのではないかと考えて,理論を発展させたのである.

このようにしてボースとアインシュタインによって確立された統計手法を「ボース・アインシュタイン統計」と呼ぶ.

今回はあまり具体的な計算手法には踏み込まず,この辺りの考え方の概要だけをまとめるだけにしておこう.

粒子の識別不可能性

粒子が全く同等であって,それぞれを別個のものだとして識別できないというのはどういうことであろうか.実はこの考えはすでに第 2 部でも取り入れてあって,場合の数の全体をで割ったりしていたのだった.しかしそれはかなり大雑把なやり方で,まだまだ正確ではないのである.まずはその辺りの説明から始めることにしよう.

とりあえず,本質をついた最も簡単な場合で説明しよう.2 個の識別可能な玉と,中を二つに仕切った箱があるとする.識別可能な玉というのは,まぁ,区別できるように玉に少しキズを付けておくか,もっと大胆に,色を塗り分けておいても同じなわけだが,何らかの違いが見出せるということである.これらを箱に入れて,ふたをして,振り回した後で再びふたを開けたときに実現している組み合わせは何通りあるだろう.

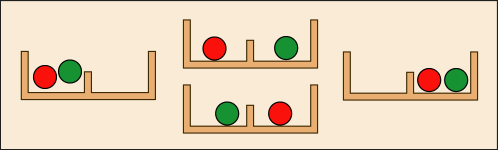
それは上の図のように 4 通りあり,出現確率はどれも 1/4 ずつだ.

では次に,識別不可能な玉を使ったらどうだろう.

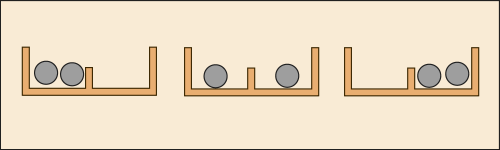
区別できない2つの玉が箱の中の二つの部分のどちらに入るかの全組み合わせを描いた図

それは上の図のように 3 通りしかない.では出現確率はどうなるかというと,我々が目に見える大きさの物体で試してみる限り,図の真ん中の状態になっている確率が 1/2 であり,残りは 1/4 となる.それは,どんなに 2 個の玉がそっくりだとは言っても原子レベルで同一なわけではなく,区別できる違いが幾らでも見出せるからである.

ところが量子力学においては,完璧に違いが見出せない状況がありうる.そして,そのような場合の出現確率はどれも同じ,1/3 ずつなのである.なぜそうなるかの理論的説明は量子力学の方に任せることにしよう.（いや,そう言えば見た覚えがないなぁ.まぁ後でじっくり調べるさ.）

ここでは仕切りのある箱に喩えて説明したが,これはそれぞれの粒子の取り得る異なる状態がたった二つしかないという特殊な状況を意味している.さて,ここでの例のようなことは本当に現実に起きるのだろうか.

これを試すためには,二つの粒子が全く区別できないようなセッティングで実験されている必要がある.例えば,右から来た粒子と左から来た粒子を順に別個に観察するような時には,このような結果にはならない.実験の対象として微小な世界の実体を使いさえすれば必ずそうなるというものでもないわけだ.

なぜうまく行っていたのか

粒子の入れ替えのみを考慮してで割るだけでは不十分であることが,今の話から読み取れただろうか.上の例では粒子が識別できる場合の状況の数が 4 通りあった.しかしそれをで割っても,粒子が識別できない場合の状況の数である 3 になるわけではないということだ.

ではなぜ第 2 部ではで割っただけでそれなりの結果が導けたのであろうか.それを考えるためには,箱の中の仕切りがたった二つきりではなく,もっと幾らでもあるような状況をイメージしてみるといいだろう.

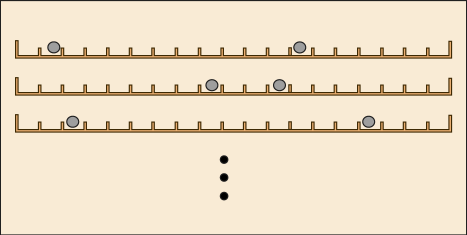
区別できない2つの玉が箱の中の多数の部分のどこに入るかの組み合わせのごく一部を描いた図

そこにばら撒かれる玉の数がそれほど多くなければ,仕切られた一つの区画の中に玉が二つ以上入ることなどは滅多に起こらない.起こったとしても全体からすれば無視できるほどだ.そういう状況では,粒子が識別できる場合とできない場合の状況の数の違いが,で割るだけでほぼ等しくなってしまう.

もし全体のエネルギーが十分に高ければ,このように粒子の取り得る状態は多種多様になり,十分にばらつくことができるのである.ところが温度が低くなり,どの粒子もエネルギーの低い状態に留まる傾向が高くなってくると,幾つもの粒子が同じ状態に入っているということが多くなり,それが無視できなくなってくる.温度だけが問題ではない.粒子の密度が異常に高かったりしても同じことが言える.つまり第 2 部で計算した例では,粒子の識別不可能性をとりあえず簡単には考慮してはいたけれども,それは温度が十分に高く,十分に希薄な粒子を仮定した場合にのみ成り立っている話なのである.

ボソンとフェルミオン

さて,ボースの発案から数年後.量子力学の基礎がほぼ確立した頃になって,さらに新しいタイプの統計が提案されることになった.それは「ボース・アインシュタイン統計」では説明の付かなかった現象をうまく説明できるものだった.この新しい統計手法はフェルミとディラックによりそれぞれ独自に提案されたので,「フェルミ・ディラック統計」と呼ばれている.

「フェルミ・ディラック統計」は「ボース・アインシュタイン統計」に取って代わるようなものではなく,ある場合には一方のやり方がうまく行き,別の場合には他方のやり方がうまく行くという,そんな関係にあった.

これら二種類の統計手法の違いは簡単である.どちらの手法も粒子が互いに識別できないと考える点では同じである.ただ,「ボース・アインシュタイン統計」では粒子が同じ状態に幾つでも入ることができると考えていたのに対して,「フェルミ・ディラック統計」では一つの状態に入ることのできる粒子はただ一つだけだという制限を付けて考えるのである.なぜ同じ状態に 2 つ以上の粒子が入れないのかという説明は量子力学の方に任せることにしよう.これは「パウリの排他律」と呼ばれる法則である.

とにかく,この世の基本的な粒子は,ボース・アインシュタイン統計に従うものと,フェルミ・ディラック統計に従うもののどちらかに分類できるのである.前者を「ボース粒子（ボソン）」と呼び,後者を「フェルミ粒子（フェルミオン）」と呼ぶ.

例えば,電子は全て例外なくフェルミ粒子である.中性子や陽子もフェルミ粒子である.一方,ボース粒子は, ${}^4 He$ や,光子,パイ中間子などがそうである.

実はフェルミ粒子かボース粒子かの違いは,その粒子のスピンの大きさに関係している.スピンの大きさが整数 ( 0 , 1 , 2 , … ) である粒子はボース粒子として振舞う.そしてスピンの大きさが半整数,すなわち ( 1/2 , 3/2 , 5/2 , … ) のものは例外なくフェルミ粒子である.このことはずっと後になってパウリによって証明されることになった.その証明は相対論的な場の理論にまで踏み込む高度なものなので今の私の手には負えないし,ここで説明すべきことでもないだろう.とにかくこれは常に成り立っていることなので安心して受け入れてもらって良い.

識別できる場合もある

この世にある根源的な粒子というのはどれも量子力学的であり,同種粒子は互いに区別できない存在なのである.ではなぜ我々の眼に見えるような大きな物体にはそういう性質が消えているかというと,そっくりに見えても構成粒子の数が違っていたり,形状がわずかに違っていたりと,色々と区別できるような違いが生じているからである.

たとえミクロな粒子であっても,区別できるような何らかの違いが付加されるようなことがあればそれらは別種の粒子として振舞う.だからどんな場合にでも同種粒子は区別できないと考えて計算するわけではない.

例えば,多数の同種粒子が集まって結晶のように並んでおり,それぞれが決まった位置の付近で振動している場合である.これは結晶の端の方のことを無視すれば,およそどの粒子も同等であると考えることができる.しかし粒子の位置によって粒子に番号を振ることができて,確実に別個の粒子であると識別することができるのである.

とは言うものの,こんな説明は気持ち悪い.ある場合には区別できて,ある場合には区別できないと言うが,一体,その違いはどこで生まれているのだろう.人間の認識の都合だろうか？それとも物理的にはっきりした違いがあると言えるだろうか？・・・それに合わせて計算方法を変えないといけないなんて,統一性がないような気がする.別に気にするようなことでもないだろうか？私は何か非常に引っ掛かる.粒子群の置かれた状況によって,粒子の基本的な性質が変化してしまっているような印象を受けるせいだろうか.

まぁ,実は物理的にはっきりした違いがあるのである.結晶のように各粒子が決まった位置に置かれている場合,表向きは全ての粒子が同等であってどの粒子も共通した条件の中から色んなエネルギーの状態を取り得るということになっている.しかし量子力学的には,位置が違うというだけですでに,「似てはいるが」それぞれ別の状態なのである.ある粒子は自由に全ての状態の中から選べるのではなく,実は自分に許された決まった範囲内でしか選べていないことになる.

だからそれらの集団が全体として取り得る状態というのは,それらの個々の粒子がそれぞれ取っている別々の状態の掛け合わせで表現されるだろう.「粒子の位置によって番号を振ることができる」という素っ気無い表現はそういう意味なのである.

まぁ,こういうのは実際に例を見てみないことには何のことを言っているのか分からないだろうから,後の方の記事で何かやってみせよう.

何が違うのか

それで結局,第 2 部でやった古典的な統計と,量子統計とでは何が違うのだろうか.実はほとんど何も違うところがないのである.本質的な差は,次の一点だけである.つまり,微視的状態の数を数えるときに,それぞれの粒子を区別することは本質的に出来ないのだと考えて,状態を重複なく数えるために何とか工夫するということ,それだけだ.

小正準集団とか,正準集団とか,大正準集団とかのアンサンブルの取り方の違いを前に説明したが,これらについても同じ論理がそっくりそのまま,何の変更もなく使える.ただ注意点は,さっきも言ったが,同じ状態であるものを重複して計上してしまわないように気をつけるということだけだ.

量子力学では状態が不連続であることが多くて,各微視的状態の数を数えやすい.それで分配関数（状態和）を計算するときに,積分ではなくて和を使うことができる.しかしこれも決定的な差ではない.量子力学の範囲の話であっても状態が連続的であることがあり,場合に応じて状態の数の数え方を工夫して計算することになるだろう.

この後の話は,その数え方の工夫を具体的にどうしたら良いかという実例の一部に過ぎない.うまく計算できるような分かりやすい例はそれほど多くはないのでどの教科書も似通ったものになっているが,それが全てではないし,本質でもないということだ.結局,ここで説明したことに気をつけながら,これから示す幾つかの例を少しだけ参考にしつつ,その場合場合に応じた上手い計算方法を編み出してゆく必要があるのである.