統計力学：光の粒子説

アインシュタイン登場

プランクの理論が認められるようになったのは,アインシュタインの活躍によるところが大きい.1905 年の 3 月,アインシュタインはプランクの理論の影響を受け,光はというエネルギーを持った粒子であるという考えで「光電効果」を説明したのであった.

さらに同じ年の 5 月,彼はブラウン運動を論理的に説明することで,原子論を世間に認めさせた.それまで原子というものは理論上の存在に過ぎないかも知れないと考えられていたのだった.ついでに言えば,その直後の 6 月,かの有名な「特殊相対性理論」を世に出すのである.立て続けに発表されたこれら三つの論文はいずれも科学史上かなり重要であり,この 1905 年は「アインシュタインの奇跡の年」と呼ばれることになるのである.

しかしプランクは,アインシュタインのこの考えには反発した.プランクが主張したのは,電磁波はあくまでも波であるけれども,そのエネルギーの受け渡しがの単位でしか行われないという内容だった.それで自分のアイデアが曲解されて広まることに危機感を覚えたわけだ.

さて,世の中にはアインシュタインの登場を讃える論調の啓蒙書が多いので,アインシュタインが主張したイメージの方が進歩的だと考える人が多いわけだが,ちょっと毒されすぎていると思う.一定の量のエネルギーの塊（これをエネルギー量子と呼ぶ）としてしかやり取りできないのならば,場合によっては,それを光の粒子が飛んで来ているというイメージで捉えることも構わないだろう.しかしそれを本当に粒子だと考えてしまうと,干渉や回折などのような波としての伝わり方の性質を説明できなくなる.そういう意味ではプランクの主張の方が慎重だとも思える.

そして現代の視点から見れば,どちらのイメージもまだまだ不完全なのだ.

粒子でもなく波でもない

ついでだから少し書いておこう.この両者のイメージのうちのどちらが正しいかというのは,光源のエネルギーをかなり低く落として行って,ひと時にたった一つのエネルギー量子しか空間を飛んでいかないと思われるような状況を作り出したときにはかなり大きな問題になる.そのとき,その塊は,波のように伝わるのか,粒子のように飛んでいくのか,ということだ.

それはどちらも正しかった.たった一つの粒であってもなぜか波のように伝わり,粒子のように検出されるのである.「粒子であるか,波であるか」という論争はもう古いのだ.それは結局のところ,粒子でも波でもなかった.それまでの人類の言葉の中になかった新しい「何か」だ.そして人類はすでに,数学でそれを表現することにある程度成功している.

その「何か」の性質をある面で見たとき,波に似た性質も見出せるし,粒子に似た性質も見出せる,というそれだけのことだ.それなのに初心者向けの啓蒙書はいまだに 100 年前の論争を引っ張り出してきて,「粒子か,さもなければ波か」と二者択一を迫り,不思議さを読者に対して突き付け,煽り立てる.

そして両者の性質がどこまでも矛盾することを徹底的に納得させた後で,最後に「粒子でもあり,波でもある」という結論に持っていって,「量子力学の訳の分からなさ」を強調する.いや,そう説明すべきではないだろう.そもそも「粒子でもなく,波でもない」のだ.

粒子か,波か,どちらかでないといけないと思い込んでいる人が多すぎる.初心者向け解説もそろそろやり方を見直すべき時だと思う.

光の圧力の別説明

アインシュタインが光を粒のように考えるようになった発想のきっかけというものがある.プランクの放射の式での大きい方へ進むと,-1 が無視できるようになって, $e^{-hν/kT}$ という形が主になってくる.一方,マクスウェル分布を思い出すと,これに良く似た $e^{- 1/2 mv^2/kT}$ という形が入っている.こちらでは粒子のエネルギーがとして入っていて,他方では,光のエネルギーがとして同じ部分に入っている.同じ形式を含んでいるのは,何らかの関連があるに違いない.実は電磁波は自由な気体のような存在なのではないか,というのである.

まぁ,場合によってはそういうイメージも真実に近くて,計算に役に立つこともある.例えば,以前に「ステファン・ボルツマンの法則」の記事中で,電磁波の持つ圧力とエネルギー密度の関係を p=u/3 だと導いたことがあったが,同じ式を粒子のイメージで前より簡単に導いてみよう.

前と同じく,一辺の立方体の容器を考える.別に 3 辺の長さを同じにしなくても問題ないのだが,その方がほんの少しだけ説明が楽だ.そして,光の粒子の運動量を (p_x, p_y, p_z ) としておこう.運動量と速度のベクトルの向きは同じなので,速度ベクトルの方はと表現できるだろう.ここで,運動量ベクトルの大きさを |p| で表してある.要するに,速度ベクトルの向きを運動量ベクトルと同じになるようにして,かつ,その絶対値がになるように調整してあるだけである.

とりあえず,軸方向の一方の壁にぶつかる光の粒子を考えると,衝突のたびに,一個あたり 2p_x の運動量変化がある.そして距離を走ってきて再び同じ壁にぶつかるには $2L\divp_x c/|p|$ 秒かかる.つまり 1 秒あたり, cp_x/2L |p| 回の衝突があるわけで,結局,1 秒ごとに $c{p_x}^2/L |p|$ の運動量変化があると言える.これを多数の粒子の分だけ和を取って,面積 L^2 で割れば,圧力となる.（圧力にも運動量にもばかり使っていて,分かりにくくて申し訳ない.）ところで,多数ある粒子のうちで |p| が同じ大きさであるような粒子ばかりを集めて,その集団ごとに平均を考えると,各方向成分には差はないので, という関係があると言えるだろう.これを代入して上の式から p_x を消せば,圧力は次のように表される. 光（電磁波）の運動量とエネルギーの関係は E=c|p| であるので,この右辺は全エネルギーを体積で割って,さらに 3 で割った形になっていると言える.つまり,エネルギー密度の 1/3 だというわけだ. さて,この例の他には光を粒子だと考える利点はあるだろうか.ああ,そうだ.コンプトン効果という現象がある.これは光が粒子であると考えないと説明しにくい現象だ.光がまるで粒子のように,他の物質粒子と衝突するのである.しかしそう考えると楽に計算できて便利な場面があるというだけであり,光が本当に粒子だと考えてしまう必要はない.正確には量子力学を使った衝突理論を適用する話になるだろう.

比熱に応用

以前に,「エネルギー等分配則」について説明したときに,その好例として「デュロン・プティの法則」という比熱についての法則を紹介したことがある.しかしその法則は低温では成り立たなくなるのだった.

アインシュタインは 1906 年にエネルギーの量子説を使ってこの問題を解決したのである.そしてその成功によって,プランクの理論も徐々に認められるようになってきた.エネルギー量子についてのプランクとアインシュタインの考えはしばらく対立したけれども.

デュロン・プティの法則については,固体元素を個の調和振動子の集まりだと考えることで説明が付いたのだった.ここでアインシュタインは,それらの調和振動子はずつでしか互いにエネルギーのやり取りができないと仮定したのである.そうなると,各振動子は次のようなエネルギーを持つしかないであろう. この条件下で,各振動子の平均エネルギーと温度との関係を導いてみよう.まぁ,これは前々回やったのと全く同じことをやればいいのである.しかしあれはプランクがなぜエネルギー量子の考え方を導入することになったのかを示すために,少し遠回りのやり方をしたのだった.前々回は小正準集団の考え方を使ったが,今回は正準集団の方法でやってやろう.

正準集団の方法では,各振動子がエネルギーを持つ確率は $e^{-E/kT}$ に比例するのだった.だから,平均エネルギーを求めるだけならば次のような計算をするだけで求められる. この続きを計算することはそれほど難しくはない.まずこの分母を見ると,これは初項 1 ,公比 $e^{-hν/kT}$ の等比数列の和を計算しているのと同じことなので,よく知られた公式が使える. さらにこの式の両辺を -1/kT で微分（慣れてない人に言っておくと,それは -1/kT を例えばなどの別の変数に置き換えてやって,で微分するということと同じである.）してやると, となり,これは分子の方と同じ形になっている.これらを合わせれば, となり,当然ではあるがプランクがやったのと同じ結果になることが分かるだろう.これは振動子一個あたりの平均エネルギーと温度との関係なので,全体の内部エネルギーは次のように表される. これをで微分して,をアボガドロ数だと考えれば定積モル比熱となる. これだと確かに温度が高くなると比熱はに近付くし,温度が 0 に近付けば比熱も 0 に近付くことが説明できる.しかし物質の種類によって 0 への近付き方に違いがあることはどうやって説明できるだろうか.もも定数なのだから,残るものといえば,物質によってやり取りのできるが違うと推論するしかないだろう.そこで他の定数もひっくるめて温度の次元に合わせた次のようなパラメータを定義する. これは物質によって異なる値を持つ定数であり「アインシュタイン温度」と呼ばれる.グラフを書くときに横軸を T/Θ としておけば,色んな物質に対して,一つのグラフの上で比較ができて便利である.

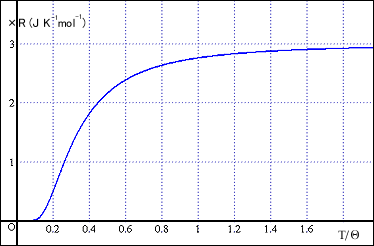
このグラフはかなりうまく現実を説明できるわけだが,残念ながら全ての物質がぴったりとこのグラフに合うわけではない.低温域でわずかなずれがある.（逆に低温域で無理やり合わせれば高温域に大きなずれが出るとも言えるわけだけど.）

それを改善する「デバイの理論」というものがある.アインシュタインは各振動子を独立したものと考える単純なモデルを採用したが,デバイは,それぞれの原子の振動が連携し合って何種類もの振動を作るという考えを導入したわけだ.ちょうどレイリー卿が考えたのと同じようなイメージだ.しかしこの理論にはレイリー卿の理論のような無限大に発散するという困難はない.原子の振動を考えているので,生じる周波数には上限があるという理屈が使えるからである.

この理論についての紹介はこれくらいにしておこう.元々,応用にはあまり深入りしないという方針だったし,ここまでの内容を学んだ読者ならば,教科書を読んで簡単に理解できるだろう.