気体の分子運動論
容器に気体が入っている.この気体は分子と呼ばれる沢山の「つぶつぶ」から出来ているのだと考える.気体の「内部エネルギー」の正体は,この分子の運動エネルギーなのだと考える.(本当は分子間力の位置エネルギーも含めるべきだが,今しばらくは理想気体を考えることにする.)また,気体の圧力は分子が容器の壁にぶつかる時の運動量変化で説明できるのだと考える.
これが「気体分子運動論」の基本的な考え方である.当時は非常に異端的な考え方であった.確かに現象の説明は出来るが決定的な証拠がない.アインシュタインがブラウン運動を理論的に説明するまでこれについて長い論争が続いていた.つまり,つい 100 年ほど前まで,この考えは完全には認められなかった.物理はそれほど厳しいのだ.しかし異端だと責められようが,考えてみることは自由だ.
この分子集団の全運動エネルギーを求めるためには分子の速度を知る必要があるだろう.とは言うものの,分子はバラバラに衝突を繰り返していて衝突するたびに速度は変わる.そんなもの,調べようがないではないか.
しかし天才マクスウェルは考えた.2 分子の衝突の結果,どちらかの分子が完全に止まってしまうなどという確率はとても小さいのではないだろうか.つまり分子集団の中で,ごく一部の分子だけが激しく動き回っていて,残りのほとんどは止まっているという状態は考えにくい.むしろ多数の分子でエネルギーを分け合うはずだ.しかし全ての分子が常にほぼ同じ程度の速度だということもないだろう.どの程度の割合の分子がどの程度の速度を持っているのか・・・その分布・・・「速度分布」が知りたい.知りたい!知りたいのだ!!
ある時は少数の分子だけが激しく運動したかと思えば,またある時は大多数の分子が平均的な速度で運動したり・・・といった具合に,速度分布は予測不能な形で常に変化を続けるものだろうか.
ごく少数の分子だけを取り出して観察していればそういうことも起こっているだろう.しかしそういう少数の分子集団を入れたカゴを沢山集めた状況をイメージしてみたらどうか.全てのカゴの中で同時に同じように速度分布が変化する可能性は,カゴの数を増やすほど低くなって行くはずだ.それで全体でみれば大きな変化は見られなくなり,一定の分布に落ち着くだろう.つまり十分な数の分子を考えれば,速度分布が時間的に変化することはなくなると考えられる・・・.
素晴らしい発想だ.しかし,その分布を知るすべはあるのだろうか?
準備
全体で個の分子があるとする.その中から一つの分子を取り出した時,その分子の
方向の速度が
くらいである確率
は,
と表せる.このように表した数式の意味が分かるだろうか.
は速度の関数で,どの速度の分子が多いか少ないかを表している.しかし速度がちょうど
だということは決してないので,ある程度の幅
を許容して考えないといけない.ごくわずかな幅の範囲では,
の値にほとんど変化はないので,幅
を広げるほどそれに比例して確率が増えると言えるだろう.これが上の式の意味だ.
これは確率なので,を 0 から無限まで変化させて積分すれば 1 になってないといけない.
このことを使ってまとめれば,全ての分子,つまり
個の分子の内,速度の
方向の成分が
の間にあるような分子の数は,
という式で表せるということだ.
速度分布の導出法
同じ議論は方向や
方向についても独立して行えるはずだ.ニュートン力学での衝突の問題は
,
,
を別々に計算しても良かったのだからそう考えて問題はないだろう.よって
方向や
方向についても関数
は同じ形をしているだろう.ということは,ある粒子の速度が
の間にある確率は次のように表せるはずだ.
ところが速度分布というのは,
,
,
軸の 3 方向の成分だけが特別なのではなく,他のあらゆる方向の速度に対しても同じ意味を持つのである.それで速度分布の関数というのは方向に関係のない「速さ」
の関数として表せる形になっていなければならないことになる.ここで私が「速さ」と「速度」という言葉を明確に使い分けていることを示すために,速さ
というのは,次のように表せる概念だということを式で書いておこう.
要するに,(1) 式は,速さ
の関数
を新たに導入して,次のようにも表せるということだ.
この式と (1) 式とを比較すれば,
というのは次のような形になっていると言えるだろう.
以上のことをヒントに
の具体的な形を推論してみよう.
もしも
も 0 だったら,
である.
が定数
だとすると,
という形になっている.つまり,
も
も定数倍違うだけで同じ形であるはずだと分かる.疑い深い人は,ひょっとして
だという可能性はないのかと思うかも知れない.もしそうなら
の大きさに関わらず
は 0 になってしまうことになるが,それは分子がある軸方向に向かってだけは運動しないという意味になってしまう.どの方向も平等なのでこの可能性は排除して構わない.
同じ形の関数の積が,やはり同じ形で表されるということと,と
,
,
の関係から,計算に慣れている人ならすぐに指数関数が思い浮かぶだろう.積の関係を和に直す時には良く指数か対数かを使うものだ.つまり,
だと考えれば,ちゃんと
になっているし,
となるから全て辻褄が合うだろう.いきなり指数関数を導入したことに論理の飛躍を感じる人もあるだろうが,ここで指数関数を使うしか選択肢が無いことを計算で厳密に導く事も出来る.ただ,それをここでやると今の議論の本質に関係ないテクニック的な要素が入り込んでしまってややこしくなってしまうのでやめた.気になって仕方無い人は,純粋に数学的,パズル的な話だから証明してみればいい.
厳密に説明しようとするとどんな面倒な要素が入り込んでしまうかを具体的に言っておこう.まず,符号や絶対値の議論を避けるために式をのように少々見づらい形で導入しておかないといけないことが一つ.この辺りに何かトリックがあるのでは,と読者が変に勘ぐってつまづくのを避けたかった.かと言って,同じような意味だからと言っていきなり
を
に書き換えてしまうのも強引だ.混乱させないためにちゃんと別の記号を用意してその関係をちゃんと説明する必要がある.こうしてどんどん脇道へ逸れて行って長くなってしまう.自分で徹底的に分かりやすく説明しようと努力してみれば,この辺りの難しさに気付くだろう.
ところで,この関数に含まれる定数が正であるとすると速度が大きくなるにつれて発散してしまう.それは速度の大きい分子が無限に見出されるという意味だ.それではおかしいので指数部にマイナスをつけた形に整えておくのが望ましい.つまり,次のようになる.
これを「マクスウェルの速度分布」と呼ぶ.しかしこの式の書き方だといかにも「速さ」の分布関数のようになっていて「速度分布」というイメージではない.この言葉の意味は,次回の記事を読むことで,よりはっきりと分かるようになるだろう.だから内容的にはこれと全く同じ式ではあるのだが,次のように書いておいた方が,式の意味する事を正確に伝えられるのかも知れない.
この式を,
だけを軸にとってグラフにすると,次のようになっている.
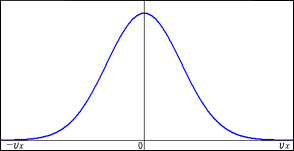
どの速度を持つ分子がどれくらいの割合で存在するのかを表しているというわけだ.一見デタラメに振舞っているように思える現象の中に全体として規則性があることを,統計的な論理だけから導き出してしまったのである!
定数の意味
確かにすごいことが分かった気がする.しかしまだはっきりしないことがある.定数は一体何を意味するのだろう.
それについてはまだしばらくは明らかにされない.これを知るためには,もう少しだけ,物理的な考察を交える必要があるのだ.普通の教科書ではそちらの準備を先にやっておくものだが,私としては,たったこれだけの統計的な考察からここまでのことが導かれてしまうのだという驚きを伝えたかったので,敢えて,いきなりこの説明から入ったのである.
一方,定数の正体についてはそれほど悩む必要はない.これは
が確率を表すという意味を保てるようにする為の単なる調整部分であり,次の条件に合うように値を決めてやればいいだろう.
単純に数学的な話だから,ここで求めてしまおう.
この変形の最後の方で,
という,良くある数学公式を利用したが,この証明をここで説明していると本題から逸れてしまうので別のページでやるとしよう.とにかく今の結果から,
であれば良いことが分かる.
吟味
しかしマクスウェルはまだ考え続けた.本当にこれは正しい論理だろうか?
彼は上で説明した他にも全く違う何通りかの求め方を思い付き,やはり同じ結論を導き出すに至った.それでこの結果にようやく自信が持てたのだという.一つの方法で満足してしまわない辺りがこれまた天才的だ.その別解についてはいずれ紹介するかも知れないし,しないかも知れない.とりあえず後回しにしておこう.
ところで今回の結論は,複数の違う種類の分子が混じっていた場合でも成り立つのだろうか?上の議論でそのような事を考察する場面が全く出て来なかったのが不思議だ.重い分子と軽い分子が混じっていれば,軽い分子の方が激しく運動するように思える.その辺りは一体どうなっているのか.
それにニュートン力学の論理を使っている様子がほとんど感じられなかった.マクスウェル分布はニュートン力学とどの程度の関わりがあるのだろうか.もし粒子がニュートン力学に従わなかったとしても同じ事が言えるのだろうか.それともこんなことは,気付いてしまえば大した事の無い問いだろうか.
色々と課題を残しつつ,次の話へと進む.










