マクスウェルの速さの分布

止まっている粒子は少ない

前回求めた「マクスウェルの速度分布」の式のグラフを見て考えてみると,どうも腑に落ちない点がある.速度が 0 のところが最大になっていて,あとはなだらかに下っているのだ.つまり,止まっている粒子の割合が一番多いという事になるのだろうか.

いや,そう考えるべきではない.前回求めたのは,あくまでも「速度」の分布である.速度の各成分が (v_x, v_y, v_z )～(v_x + dv_x, v_y + dv_y, v_z + dv_z ) の間にあるような粒子の割合を表している.そう言われても,「やはり速度が 0 である粒子が一番多いという意味には違いないのでは？」と考えたくなるのが普通だろう.しかしそれは違うのだ.

「速度」ではなく「速さ」で考えてみよう.速さが 0 である状態を速度成分で表すと, (0,0,0) のたった一通りしかない.しかし例えば,速さが 1 である状態の数はどうか？ (1,0,0) (0,1,0) (1/√2 ,1/√2 ,0) ・・・などのように,無限に何通りでも考え付く.状態の数に無限の開きがある.つまり,ある「速さ」で動いている粒子の「速度」状態の表し方は多数あるため,それらを合計した実現確率というのは非常に高くなっている.一方,速度 0 の状態の実現確率は単独では最大になっていても,たった一通りしかない.それで,前者は後者を圧倒的に凌いでいることになる.

しかし・・・状態の組み合わせが無限にあると考えてしまうと合計の確率が無限になる気がしてしまってまずいな・・・.別の説明をした方が良さそうだ.

速度空間

同じ速さを表す速度状態がどれくらいあるかを視覚的に理解する為に,速度の 3 つの成分をそれぞれ空間の 3 つの座標に見立てて考えてみよう.こういうのを「速度空間」と呼んだりする.速度を表すベクトルが,あたかも空間内での位置を示しているかのように考えるのだ.この速度空間の中で一点を指し示せば,それは速度の 3 成分の大きさを指定した事になる.

速さが 0～ dv の範囲にある状態というのは,この空間の中で考えると,どの部分を占めるだろうか.それは原点を中心とした半径の球であり,その体積 4/3 π dv^3 の範囲内に含まれる状態がその条件に当てはまっている.では次に,速さが v～v+ dv であるような状態というのは視覚的にはどう表せるだろうか.それはまず半径 v+ dv の球を考え,その内部から,半径の球の部分を除外した部分となる.すなわち,厚みの球殻として表される.その体積は次のようにして計算される. ただし幅は非常に小さいと考えているので, dv^2 や dv^3 などの項は取るに足りないものとして省いてしまった.

この結果を見ると,が大きいほど,その付近の v+ dv までの範囲に含まれる状態の割合が格段に多くなることが分かる.試しに v=0 を代入すると dV=0 となり,最初に求めた 4/3 π dv^3 とは一致しないので不審に思うかも知れないが,それほどまでに取るに足りない存在だという意味だ.

この辺りの体積比を考慮して,粒子の「速さの分布」を導き出してみるとしよう.

速さの分布の導出

その計算は大したテクニックを使う事なく終わらせることができる.まず,速さの分布関数を P(v) で表すことにしよう.こうしておけば,速さが v～v+ dv の範囲にあるような粒子の数は, P(v) dv に比例すると表せることになる.

前回求めたところによると,ある速度を持つ粒子の存在確率は $A e^{-bv^2}$ に比例しており,それと同じ速さを持つ粒子の存在確率はみな同じ値になっている.そこに,先ほどの速度空間の体積比の考えを合わせれば,同じ速さを持つ粒子の数は $A e^{-bv^2} ×4πv^2 dv$ に比例するという表し方ができるだろう.これは P(v) dv と同じ意味であるので,定数部分をみんなとしてしまえば,次のようになる. これが「マクスウェルの速さの分布」の式である.これをグラフにすると次のようになる.

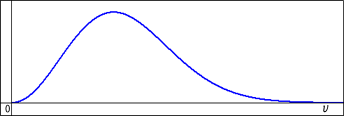
なかなか面白い特徴を持った形であろう.止まっている粒子というのがほとんどないということも読み取れる.もし定数の値の意味が明らかになったならもっと楽しい物理の説明ができるのだが,今はまだやめておこう.

係数についてはが成り立つように決めてやればいいだけの話だ.これを計算する為にはという公式を使えば楽なものだが,この証明は別のところでやる事にしよう.とにかくこれによって, としておけば良いことが分かる.

名前がかぶってるよ

これでマクスウェルの「速度分布」と「速さの分布」が全く違うものであることが分かった.

ところで,前回の記事に出ていた「速度分布」の式とグラフを良く見直してみると・・・あれれ？これって,数学や統計学に出てくる「正規分布」と同じ形なのではないか？正規分布というのは別名「ガウス分布」とも呼ばれているのだった.その詳しい意味については数学の教科書で学んでみて欲しい.

同じ形の分布を表すのに呼び名は幾つも必要ない,というので,物理以外の分野で「マクスウェル分布」という言葉が使われるときには,今回求めた方の「速さの分布」の式のことを意味する場合が多いようだ.

では物理ではその辺りの区別はどのように付けているかというと,「どっちのことを言っているのかくらい,前後の文脈を見て自分で判断しろ」ということになっている.いや,何とまぁ,厳しい世界ではないか.

積分の変数変換

ところで「速度分布」の式と「速さの分布」の式とを見比べてみると,係数もそのままで,ただ 4πv^2 を掛けただけの違いしかないという事が分かる.それもそのはず,これらは数学的には単に積分変数の変換をしただけのことであり,先ほどは全く違うものだと書いたが,実は全く同じものであるという見方も出来る.

いきなりそのような数学を使うと煙に巻かれてしまう読者もいるだろうと思って,ここまではじっくり意味を考えるような遠回りの説明を敢えて選んできたのである.一旦分かってしまえば,数学を使ったやり方の方が,よっぽどすっきりする.

例えば,速度分布については次のような積分の関係式が成り立っている. これは速度空間の全域を覆い尽くすような積分である.これを 3 次元の極座標 (v,θ,φ) を使って,同じ空間を覆い尽くすように表し直してみよう.次のような変換で,上に書いた式の左辺の積分を書き直そうというわけだ. 積分変数の変換にはヤコビアンというものを使うが,その辺りのテクニックについては数学の教科書で学んで欲しい.とにかくヤコビアン |J| は微小領域の体積比,あるいは面積比などを表しているのであり,今回のような 3 次元極座標では, となる.これを使えば, となり,速さの分布が 4πv^2 F(v) と表されることが簡単に分かるというわけだ.