レイリー・ジーンズの理論

探求は続く

ウィーンによる考察は熱放射の研究に重要なヒントをもたらしてくれた.いや,それだけではない.彼の部分的な成功は更なる探求への意欲を掻き立ててもくれたのだった.（ずっと後になるが,彼はこの件でノーベル賞を受けてもいる.）しかし彼のやり方は外面的な観察結果からぼんやりと中身を推測したようであり,今ひとつ本質に切り込めていない印象も受ける.

レイリー卿もそのような不満を感じていた一人であった.彼はもっと根本的なところからこの現象を解き明かしたいと考えたのだった.ところでレイリーというのは彼の本名ではなく,爵位に伴った通称であるから,歴史と位に敬意を込めて今後もレイリー卿と呼ぶことにしよう.レイリー卿は電磁波に対して統計力学の手法を当てはめることを思い付いて試してみた.結果から先に言うと,彼の理論は完全には成功しなかったのである.

それでも彼の理論をここで知っておくことには大きな意味があると思う.それは,彼の考え方・・・統計力学の使い方が全く正しかったからだ.にもかかわらずうまく行かなかったのは,まさに古典力学の限界なのである.それで,正しい考え方,正しい統計力学の応用の仕方というのがどういうものなのか,そしてそれのどこがうまく行かなかったのかを知っておくことにしよう.

もちろん,彼が最初から正しい考えにたどり着いたわけではないことは科学史を調べると分かるのだが,その辺りは分かりやすく修正して,すっきり説明したいと思っている.

彼が発表した論文では定数を求める部分に少しの誤りを含んでおり,数年後にジーンズによって正しく修正されたので「レイリー・ジーンズの理論」と呼ばれるようになっている.レイリー卿とジーンズはこの問題について以前から討論を重ねているので,ジーンズが後から出てきて成果を横取りしたという感じではなく,ある意味で共同研究者のようなものだと考えるのがいいかも知れない.

ウィーンの理論の弱点

ウィーンの理論は低い周波数の側では観測と合わず,少しばかり惜しいことになっていた.しかしこれは決して惜しいなどと呼べるものではなく,物理的には大きな問題を含んでいるのである.レイリー卿はそれを見抜いて,ウィーンの理論の弱点を批判した.一体どこがそんなにまずいのだろう.

前回の説明では分かりやすいようにと思って,周波数で区切る方法で説明した.しかし同じ内容を,波長で区切る方法で議論したらどうなるだろうか.ここではやらないが,結局は同じ内容の結果を導けるのだ.それについては読者にお任せして,ここでは変数変換によって手っ取り早く求めてみよう.波長と周波数の関係は ν=c/λ であるから, となる.これを前回のウィーンの放射公式に代入すれば, となる. | dν| のように絶対値の記号を付けてあるのは,今は微小幅の大きさだけが問題で,その変化の向きは気にする必要がないからである.これがないと全体がマイナスになってしまって気持ち悪い.さて,これにより, λ～λ+ dλ の波長範囲にある電磁波のエネルギー密度は, という式で表せるということになる.これをグラフで表してみよう.

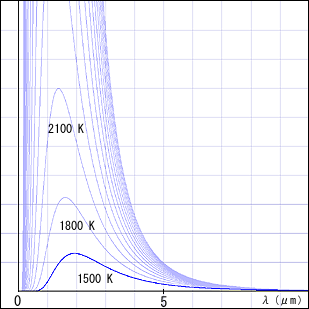
前回のグラフとは違って左右の意味が入れ替わる.ピークより右側の部分が周波数の低い電磁波であり,ウィーンの理論の弱点の部分である.明らかに何かがおかしい.温度がどんなに高くなっても,ピークより右側の曲線が一定以上に上がらないのである.

一見,細分化された各波長ごとにウィーンの変位則が成り立つという条件に反しているかのように思えるかも知れないが,数式の上ではちゃんと辻褄が合っているので,気になる人はじっくり考えてみて欲しい.とにかく,数式上は問題ないが物理的には何かがおかしいということだ.

この話は今回のメインの話とは関係ない.おまけみたいなものなので,さっさと次へ進もう.

エネルギー等分配則を使う

レイリー卿の理論は実に単純である.熱平衡にある空洞の中では様々な電磁波が存在を許されている.それぞれの波がどれだけのエネルギーを持っているかは予想が付かない.電場や磁場の強度が分かれば電磁気学を利用して計算は出来るのだが,今はそれが分からないのだ.

しかし統計力学には「エネルギー等分配則」というものがあって,それによると,力学的な振動子の 1 個あたりに平均ずつのエネルギーが配られるのだった.

熱平衡になっている状態を考えるのだから,電磁波は空洞の中で定在波として存在していることだろう.それはきれいなサイン関数で表される振動をしており,力学的な振動子と同じようなものだと考えられる.一つ問題があるとすれば,それは古典力学の問題としてだけ証明されたこの法則を,電磁波にそのまま適用しても大丈夫かどうかということだ.実は大問題である.

実はこの点には明確な根拠はない.当時は電磁波というものがエーテルの力学的振動であると信じられていたので,このような無茶な仮定にもそれなりの説得力があったと思われる.

ちょっとおかしな教科書では,多分著者の思い付きで書いてあるのだろうが,電磁波のエネルギー密度が $1/2 ε_{0}E^2 + 1/2 μ_{0}B^2$ であって,これがエネルギー等分配則の証明で使った全系のエネルギーと同じ形式だから,それぞれの項に kT/2 ずつのエネルギーが分配されることが言えるなどという,首を傾げる説明がしてあることがある.化学系とか工学系とか,とにかく物理系でない教科書に多い.そういう教科書は伏せておこう.え？物理系の教科書ではどうなのかって？そりゃあ,この点はさらっとうまいこと言い逃れてて,そこが面白いのだ.

レイリー卿の理論には,当時,固体比熱の説明に成功して注目を集めていたエネルギー等分配則が,一体どこまで通用するものなのかという,統計力学をテストする意図もあったわけだ.

さて,あまり考えなくても分かることだが,空洞の中の定在波なんて,幾らでも無限にある.もう少し詳しく説明しようか.壁と壁との間で,両端がちょうど 0 になるようなサインカーブを考えたらいいわけだ.波長が長い場合には,この条件に合うものはそれほどはないだろう.しかし波長が短い方へと考えを進めれば条件に合う波は幾らでも見つかる.波の種類が無限に多くあるということは,割り振られるエネルギーも無限である.空洞の中に無限のエネルギーがあるわけはないし,温度を少し上げるにも無限のエネルギーが必要だということになる.これはおかしい.

もちろんレイリー卿は最初からこのことに気付いていたのだが,それはエネルギー等分配則にまだ知られていない適用限界があるためだろうと考えた.周波数ごとに細分化して,その狭い範囲内で条件に合う波の数を数えるならば,それは無限にはならないし,周波数が低いところではきっとうまく行くだろうと楽観的に取り組んだわけだ.

定在波の種類を数える

では,どれだけの種類の波が存在し得るか,数え上げてみよう.こういうときには,一辺の長さの立方体の箱を考えるとやりやすい.

考える箱の形によって波の数が違ってきてしまうのではないかという心配があるかも知れないが,これは 20 世紀に入って数学的に解決した.確かに空洞の形によって波の数にわずかな違いが出るのだが,主要な項はどんな形の場合でも変わらず体積に比例するので,体積が大きければほとんど問題はないということである.1910 年にローレンツが予想し,1912 年にワイルが証明したそうである.

,,のいずれかの座標値が 0 またはになるところで 0 となるという境界条件でマクスウェルの波動方程式を解いてやればいいのだ.結果は次の通りである. これが一体,どんな波であるのかを具体的に頭の中に思い浮かべるのはそれほど難しいことではない.どんな形なのか,なぜこんな解になるのかということを考えるのは大切ではあるが,今回の話の中ではそれほど重要ではないので,読者にすっかり任せてしまうことにしよう.

とにかく, (n_x, n_y, n_z ) の 3 つにそれぞれ整数を入れた組み合わせの数だけ,違った種類の波が存在するというわけだ.そしてその周波数もその 3 つの整数の組み合わせで決まるのである.もう一つ大事なのは,ベクトルの存在である.これは波の進行方向に対して垂直な面内のベクトルであり,どの方向でもいい.要するに偏光を表している.つまり 2 つ分の自由度があるわけだから,波の数も最終的に 2 倍して数えてやらないといけない.

以上の情報から,周波数が ν～ν+ dν の範囲内にある波の数を数えてみよう.そのためにはこうすればいい.

まず,3 次元座標を思い浮かべ,それぞれの軸が (n_x, n_y, n_z) を表していると考える.この座標空間内での 3 つの数字が正の整数になる場所に玉を置くとすると,縦横高さの方向に一定間隔でズラーッと並ぶことになるだろう.この玉の存在一つあたりに 2 種類の波が存在することを意味している.この玉の存在する密度は,この特別な空間の単位体積あたり,1 個である.

一方,周波数がであるというのは,この空間内においては,原点から距離 r=(2Lν)/c だけ離れているということである.すると, ν～ν+ dν の範囲というのは,距離が (2L)/c ν～ (2L)/c (ν+ dν) の範囲にあるということだ.距離 r～r+ dr の範囲にある球殻の体積は 4πr^2 dr であり,変数変換してやると, 4π(2Lν/c)^2 ×(2L/c) dν である.今は各座標が正の範囲に限るのだから,その 1/8 の球殻を考えればいいので,微小体積は (4πL^3/c^3) ν^2 dν ということになる.

この中に含まれる玉の数は,密度を掛ければいい.密度は 1 だからそのままだ.そして玉の一つにつき 2 つ分のカウントをしてやるので,結局, だということになる.

紫外発散の問題

ここまで来たら,あとは簡単だ.一種類の波ごとにずつのエネルギーが分けられるのだから,この波の個数にのエネルギーを掛けてやれば,箱の中にある微小な周波数範囲の波のエネルギーが求められる.さらに,エネルギー密度を知りたいので,体積 L^3 で割ってやればいい.こうして導かれるのが,「レイリー・ジーンズの放射法則」と呼ばれる式だ. この結果を,実測値と比較できるようにグラフにしてみよう.

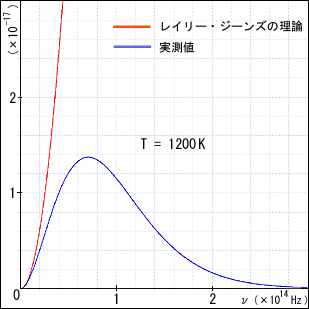
周波数の低いところでの立ち上がり部分は見事に一致することが分かる.前回のウィーンの放射法則ではうまく行かなかった部分である.今回,特に素晴らしいのは,実測値にうまく重なるように係数を調整したわけではないというところだ.正しい係数を理論的に導き出すことに成功しているのである.

しかし残念な点は,予想通りではあるが,周波数の高い側ではまったく実際と合わないことである.紫外線の方向へ進むにつれて無限大へと発散してしまうというこの問題は「紫外発散」と呼ばれることになった.これでは全周波数に渡って積分したときに無限大になってしまい,ステファン・ボルツマンの法則さえ説明できないことになる.

それでもこの式は,ウィーンの示した条件を満たしてはいるのだ. という具合に.

あらゆる周波数領域で正しい放射の密度を導くことの出来る理論を作るには,一体,どんな考え方を導入したらいいのだろうか.