ロバートソン・ウォーカー計量

時空への別のアプローチ

一般相対論は時空を研究するための足掛かりをくれた.要するに,計量を求めてやりさえすればいいわけだ.

シュバルツシルト解では最初に質量分布（エネルギー運動量テンソル）を設定してやってそれに合う計量を導くという手順を取ったわけだが,逆のやり方を選んでみてもいいだろう.最初に幾つかの条件を付けて計量の形をかなりの程度決めてしまってから,その形を実現するようなエネルギー運動量テンソルは一体どんな形であれば良かろうか,と探してやるのである.

シュバルツシルトは一つの天体の周りの時空の形を求めたのだった.しかし今回は,それとは比べものにならないほどずっと大きな事を考えてみる.宇宙全体の時空の形を導いてみようではないか.

球面のような閉じた宇宙

我々の住むこの宇宙の空間が曲がっていると考えることにする.曲っていないとすれば一般相対論を考える意味がほとんどない.どのように曲がっているかが問題だ.

広い目で見れば宇宙はおそらくどこでも同じだろうから,どの場所も同じくらいの曲率で曲がっているとしてみよう.イメージとしては,球の表面である.球面上のどこであろうと他に比べて特別な場所ではない.球の表面に住んでいる人は自分ではまっすぐ進んでいるつもりなのに,どこまで行っても世界の果てにはたどり着かずいつの間にか元の場所に戻ってきてしまう.

相対論では「時間軸も含めた 4 次元時空」が曲がっていると考えるのが普通だが,今回の話では空間の 3 次元だけが曲がっていると考えることにする.時間が遠い未来と過去で一周してつながっているという不思議な話には飛びつかないようにしておこう.

なぜそのように考えるのかと言われても,この辺は仮定に過ぎない.今はどうこう言っても仕方がない.計算が終わった後でこの仮定が妥当かどうかもう一度考え直してみることにしよう.

曲がった 1 次元の世界

話を分かり易くするために 1 次元から順に考えて行ってパターンをつかむ方法を取ろう.

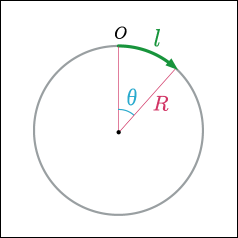
まずは 1 次元の世界,つまり一本の線の上で生きている住人を考える.1 次元の住人は自分のいる場所を表すのに一つのパラメータしか使えないから,自分たちの世界が曲がっているなどとは思いもしない.しかしある程度の距離を進んでいくと,なぜか元の場所に戻ってくるというのである.

彼らには全く思いもよらない発想だろうが,これは輪を描いていると考えるより他ない.この輪がどの場所でも同じような曲がり方をしているとすれば,その輪というのは真円である.円を考えるには次元を一つ増やしてやって 2 次元の世界で考えるしかない.円の方程式は 2 次元の世界で次のように表される. この円周の上だけを移動する 1 次元の住人にとってはは定数である.だから自分の位置を 2 次元のデカルト座標 (x,y) で表すよりも極座標に書き換えておく方が変数が減ってありがたい. こういう関係を設定しておけば常に (1) 式を満たすわけだ.

ところで「曲がっていない 2 次元の世界」つまり「真っ平らな世界」では,わずかに離れた 2 点間の距離はデカルト座標を使って次のように表される. これを極座標で表すためには,やが変化したときにとがそれぞれどれだけ変化するかを計算してやれば良い. これらを代入すれば,だけ移動した時の距離が求められる. これが「平らな 2 次元」の上に極座標を引いたときの計量である.しかし今考えている「曲がった 1 次元」の世界ではは変化しないので次のようになる. 最初から dR=0 としておけばここまでの計算はもっとずっと楽にできるのだが,あとの方で (2) 式を使いたいためにちょっと回り道をしたのである.

さて,ここまで求めたのはいいのだが,1 次元の住人にとってなんて変数は全く馴染みがない概念だ.2 次元の住人から「というのは曲がった 1 次元の世界の上のどの点からも等距離にある別次元の場所から見た角度を表す」などと説明されても彼らにはさっぱり理解できない.そこで 2 次元の住人は仕方なく「それは 1 次元世界での距離との間に l=Rθ という関係があるものだ」と教えるだろう.

すると dl=R dθ だから,結局はと「翻訳」されることになる.ああ,なんと当たり前すぎてつまらない結果だろう.1 次元の住人にとっては,自分たちの世界が曲がっているかどうかなんて本当には知ることができないのだ.

曲がった 2 次元の世界

2 次元の住人と付き合うのはもう少し面白い.

彼らは球面の上に住んでいるが,自分たちの世界が平らな平面だと信じていた.しかし球面上の広い範囲を行き来するようになって何かがおかしいと気付き始めたのである.平行線を引いたつもりでも,長く延長してゆくにつれて幅が変わってしまい,広い範囲をデカルト座標で正しく覆い尽くすことができないことに気がついた.また,大きな円を描くと円周率がずれてくることにも気がついた.

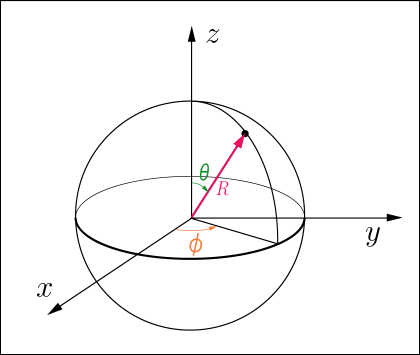
これらの現象を理解するには 3 次元人の助けを借りないといけない.この 2 次元世界は 3 次元の球の表面に存在しているというのだ.球面は次の方程式を満たす. 球面というのは半径が一定であるような場所なので,極座標で表しておけば変数が減らせる.3 つの座標変数 (R,θ,φ) の内のは定数になるからだ.次のような変換を導入しておけば,やがどんな範囲を動こうとも常に (3) 式を満たしている. これを図で表すと次のような状況である.

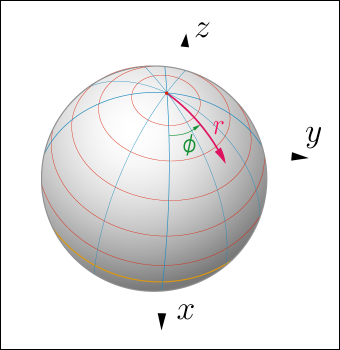
あとは 1 次元の場合と同じことを繰り返せばいい.計算の手間は増えるが計算内容は初歩的なので,ここでは途中の計算をすっ飛ばして結果だけを書いておこう. これは「曲がっていない 3 次元」の計量である.球面上で移動する限りは dR=0 だから,「曲がった 2 次元」の上での計量は次のように表されることになる. しかし 2 次元の住人は自分たちの世界での位置を二つの角度変数ととで表すことには不慣れで当惑している.そもそも球などというものの形を想像することが難しいのだ.彼らがもし極座標を使ったとしても,球面上の一点を原点と定め,そこからの方位をで表し,そこから球面に沿って進んだ距離をとしたものを考えることだろう.

そこで 3 次元人の知恵を借りることにする.3 次元人の説明によれば,2 次元人の使っているは 3 次元でも同じ意味なのでそのまま (6) 式に当てはめて使えるそうだ.そして 2 次元人の使っていると (6) 式で使われているの間には r=Rθ という関係があるそうだ.なるほど,そういうことであれば「翻訳」ができそうだ！は定数だから dr=R dθ だろう？すると (6) 式は次のように書き換えられる. なるほどねぇ.2 次元人は以前は自分たちの世界が平坦だと思っていたから,(2) 式のような形になると考えていた.ちょっとまずいな・・・.(2) 式で使っている変数はここでの話と噛み合っていないので,今の 2 次元人の立場に合わせて書き換えておこう.こういうことだ. これと比べると (7) 式はずいぶんと違った形である.もちろん,がとても小さい場合には sin(r/R) ≒ r/R と近似できるから (7) 式と (2') 式とは同じ形になっている.2 次元人の行動範囲が狭かった時代には (2') 式を使っていても良かったのである.

さて,これで全て解決かと思われるのだが,(7) 式の複雑さが少し気に入らない.2 次元人はこれを次のように解決した.

2 次元人は自分たちの世界に描いた円の円周の長さを (7) 式を使って正しく導くことができる.円周というのは dr=0 だから (7) 式は ds=R^2 sin(r/R) dφ となる.を一周させればだから,円周の長さの合計は 2πR^2 sin(r/R) だと求まるわけだ.この値が 2πr からずれているため,この世界での円周率はにはならないのである.

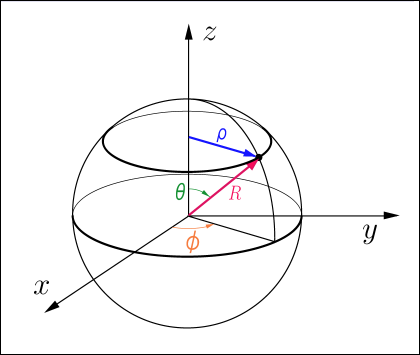
では円周の長さを基準にして極座標の動径の目盛りを定める新しいやり方を導入したらどうだろうか.原点を中心に描いた円の円周の長さが 2πρ であるとき,を原点からの距離として使うのである.まず円周の長さを測って,それをで割る.その値を動径からの目盛りとして採用するわけだ.3 次元の立場から見るとこのというのは次の図のように表される.

との間には次のような関係があることになる. だから, と計算できて,これを (6) 式に当てはめると次のようになる. もちろんは実測の距離とは値がずれるので 2 次元人の実生活には不便が生じると思うのだが,科学的な計算の都合からすると確かにこの方が (7) 式よりも楽なのだ.

これでもまだ複雑だというのなら,曲率 K=1/R^2 を導入してやればもう少しすっきりするだろう. もしこれらの計量を使ってリッチスカラーを計算することにチャレンジしてみたなら,(6),(7),(8) 式のいずれを使ったとしても結果は同じ 2/R^2 になるだろう.このようにリッチスカラー曲率の値は使う座標に関係なく世界の曲がり具合を示してくれるので同じ値が出るのである.

ああ,こりゃいかん！リッチスカラーのと球の半径のとで記号が同じになってしまうことに今更気がついた！ここでリッチスカラーを求める具体的な作業を示すと記号が混乱してしまうので,こちらの別記事にて記号を変えてやることにしよう.

報告：このサイトのリッチスカラーの解説のところでは,「ここで使っている定義では R = - 2K という関係になっている」と説明していましたが,今回この記事のために丁寧に計算してみたところ,このサイトの定義でも R = 2K となるようです.嘘を書いてすみませんでした.

注意：リッチスカラー（ここでは R_s とする）とガウス曲率 K との間に R_s = 2K という関係が成り立つのは 2 次元の場合だけである.n 次元では R_s = n(n-1)/R² になるそうだ.例えば 3 次元の球面の場合にリッチスカラーを計算すると R_s = 6/R² という結果が出るはずだ.

曲がった 3 次元の世界

さあ,いよいよ 3 次元の番である.我々には 4 次元からの助けはあるのだろうか.たとえ 4 次元の住人に何かを教えてもらったとしても「はいそうですか」と受け入れて納得することなどできない.できる限り自力で考えてみよう.

4 次元球は平らな 4 次元の世界の中で次のように表される. ここで 4 番目の軸としてという記号を使っている.もしを使ったら時間軸と勘違いされる可能性があるし,だとまるで速度を表しているかのようだ.それでアルファベットを遡ってを選んできた.は他の 3 つの軸と全く対等な軸だと言いたい気持ちを受け取って欲しい.

今までのパターンから考えて,次のようにすれば,この式を常に満たすような極座標が作れそうだ. 数式としては確かにこれで条件を満たすわけだが,イメージできないものをあたかも見てきたかのように使うことに無責任さを感じないわけではない.ここで新しく導入した角変数は一体どこの角度で,どんな範囲を動くのだろうか.

3 次元の極座標の場合は図に表すことができたから,の動く範囲が 0～2π で,の動く範囲が 0～π であると堂々と説明することができた.しかし 4 次元の把握は難しい.などというものを勝手に導入したりしたせいでどこかに辻褄の合わないことが起きたりしないかは心配なところである.

図を描くのは諦めるが,論理で何とかしてみよう. (x,y,z,u) の組みを決めて 4 次元の中に一点を定めたときに,その同じ点を表すための (R,ψ,θ,φ) がいつでも一通りに定まるように角変数の範囲を制限してみよう.要するに,4 次元空間の全体を極座標を使って「もれなく,だぶりなく」覆い尽くせることを確認しておきたいのだ.

3 次元球の極座標を参考にすればそれほど難しいことはない.の動く範囲は 0～2π であるが,の動く範囲は 0～π に制限されていた.その理由は図を見れば明らかだが,論理的にも考えてみよう.もしが,制限されているを少しだけ越えて π+α になったとしたら・・・？(4) 式を見るととには sinθ というパーツが含まれているが,それらが sin(π+α) となれば,もも負の値になる.符号が逆転することさえ気にしなければ,これは制限範囲内の sin(π-α) という値でも代用できる.一方,に含まれる cosθ は cos(π+α) と cos(π-α) のどちらを使っても何も変わりがない.を 180°回転させてやればとだけ符号を変えてやることができるので,は 0～π の範囲に限定してやっても同じ表現ができるわけだ.

(9) 式の変換も同じような構造になっている.により少し大きな角度を入れてやると,,の符号が変化する.それをととが協力して打ち消すことができればいいわけだ.を 180°回転させてやればとの符号が変わる.そしてを π/2 を中心に反転させてやればだけ符号が変わることになる.このようにしてには 0～π の範囲があれば十分であることが理解できる.要するに,(9) 式の場合にはの動く範囲が 0～2π で,の動く範囲が 0～π で,の動く範囲も 0～π としておけば十分だと言えるわけだ.

ちょっと長い脇道に逸れてしまったが,こうして想像しにくい「4 次元の極座標」にも説得力が出てきたことになる.先へ進むことにしよう.(9) 式を使って計量を計算するのは項が増えてかなり面倒だが,手順はこれまでと同じであり難しいところは全くない.結果は次のようになる. 3 次元の住人はが変化する方向には動けないので,「曲がった 3 次元の計量」は次の形になる. これが我々が必要としていた「球形に曲がった 3 次元」の計量である！

・・・と言われても嬉しくも何ともないだろう.我々は 3 次元の位置を表すのに 3 つの角変数 (ψ,θ,φ) を使うことに慣れてはいない.そもそも意味不明だ.我々が使いやすい変数に翻訳して欲しいものである.

しかし 4 次元人の助けは必要ない.今までのパターンから十分推理が可能である.まず (4) 式を見よう.2 次元人にとっての原点,つまり θ=0 かつ φ=0 の地点から,だけを動かした場合には,それが示す場所は少しも変化しないのだった.だけを動かせば,それは 3 次元球の大円コースをたどることになるのである.

(9) 式を見ても同じ構造になっている.我々 3 次元人にとっての原点は (ψ,θ,φ)=(0,0,0) だとしよう.そこからだけを動かしても,だけを動かしても少しも移動しないことが分かる.しかしだけを動かせば軸と軸が変化して,我々の原点を通る 4 次元球の大円コースをたどることになる.だから我々 3 次元人にとっての動径ととの関係は r=Rψ だろうと言えるのである.これを使って (10) 式を書き直してみよう. が小さい時には sin(r/R) ≒ r/R という近似が成り立っているのだったから,それは (5) 式の,曲がっていない 3 次元での計量と同じ形になる. 我々の行動範囲が狭い間は,我々は自分たちの世界が曲がっていないと信じていることが出来るのである.ところが大きな円を描けば円周率はよりも小さくなるし,大きな球を考えればその表面積は 4πr^2 よりも小さくなるというわけだ.

想像してみて欲しい.我々が,自分のいるところから一定の距離にある壮大な天球を考える.その天球に畳か何かを敷き詰めるなどして面積を実際に測ってみると 4πr^2 より小さいのである！遠くの方へ行くほどにすぼまっている感じだ.

全方向に向かって飛び出していった多数のロケット船団は,の距離だけ旅した先の一点で再び遭遇するのである.そこが宇宙の反対側だ.遠くへ行くほど狭くなる世界！閉じた世界！正反対まで先を考えると天球の面積はついに一点にまで縮むのだ.

さて,我々も (11) 式を簡素化することを考えてみよう.その為には動径座標を犠牲にするのだった.もはや動径が実際の距離を表すことにはこだわらず,新しい動径を使った場合に円周が 2πρ になり,天球の面積が 4πρ^2 になるように調整するのである.それは結局,次のような形であればいいわけだ. (10) 式と比べてみれば, ρ=Rsinψ であればいいことになる.計算すべき内容は 2 次元の場合と全く同じであって,結果はこうである.

宇宙全体の膨張、収縮

次は時間軸との関係を考えないといけない.宇宙のすべての場所は一様であるとの仮定から始めたのだから,場所によって時間との関係が変わるようではいけない.しかし時間によって関係が変化することについては禁止していない.それで,次のような形が考えられるだろう. ついに到達した！これが「フリードマン・ルメートル・ロバートソン・ウォーカー計量」である.あまりに長いので頭文字だけをとって「FLRW計量」と表記したり,二人分の名前を省いて「ロバートソン・ウォーカー計量」と呼ばれることも多い.

ここで使っている a(w) は「スケール因子」と呼ばれている.これは物理的にはどういう意味を持っているのだろう.

もし a(w) が倍になったとすると,次のように変形できる. 結局, a(w) が倍になったことの影響は,曲率が 1/b^2 倍になるのと同じことであることがわかる.すなわち宇宙の半径が倍に膨らんだということである.動径のスケールがからに変わってしまっているが,というのは実際の長さを表すものではなく,に比例して変化する量であるのでこうなって当然である.

こうしてこのロバートソン・ウォーカー計量が,宇宙全体が膨張や収縮をすることを許すものであることが分かる.宇宙の曲率を時間の関数として取り入れてもいいのだが,同じことが a(w) を変化させることによっても表せるので,その方が簡単である.現在の時刻を $w_{0}$ として, $a(w_{0})=1$ としておけば,は現在の宇宙の曲率を表すことになる.

宇宙時間

ところで,ここで使われている時刻というのは誰にとっての時間を表すのであろうか.宇宙では色んな運動をする物体があり,それぞれの運動状態によって時空に対する立場が異なるのであった.全宇宙に共通な時刻など有り得ない気がするのだが・・・.

これについてはこう考えるより仕方ないのではないか.我々は宇宙全体が均等であるという仮定から出発した.しかし宇宙の細かい部分に注目すれば,そこには様々な銀河が存在しており,それらに含まれる星々の質量やその激しい運動によって時空はあちこちで激しくねじまがっているはずだ.中にはブラックホールもあるだろう.しかしそういう狭い部分の激しい変化には目をつぶって,宇宙全体規模での均された様相に目を向けるわけだ.星々がまばらな領域ではそのような状況に近い穏やかな場所も多くあるに違いない.ここに出てくるというのはそういうところで流れてきた時間だと考えるのである.

宇宙全体から見れば銀河内の物質の激しい動きを小さなものとして無視できるとしても,その無数の銀河がもし宇宙全体を激しく流れていたとしたらどうだろう？その流れに乗った観測者の感じる時間が正当性を持つのだろうか？それとも,それらの動きを無視した静止系みたいなものがこの宇宙に存在しているのだろうか？そもそも相対論はこの宇宙に特別な基準となる慣性系のようなものは存在しないと主張していたのではなかったか.

宇宙に存在する物質の全体に重心と呼べるものがあるだろうか.もしそういうものがあれば,それを宇宙全体で共通の基準に出来てしまいそうだ.今回のイメージで考えるなら,球の表面を物質が流れているようなものである.その球の表面のどこかが重心であると決められるだろうか.そういう一点は決められそうにもないが,全体が同じように流れていれば,それらが流れていないように見える神の視点みたいなものはありそうだ.はそういう視点に乗った場所での時間だと言えるのではないだろうか.

そう言えば,近頃の観測で宇宙の背景放射が宇宙の全方向で一様であることが分かったのだった.ただしそれは,銀河の運動と太陽系の運動に乗っかっている地球の動きの影響を差し引いた上での話である.ということは,背景放射が全方向で一様に見えるような系というものがあるということだ.今回の計量で基準としているのはそういう系ではなかろうか.そういう宇宙の絶対座標のような系があったとしても,物理法則が系によって異なるようなことさえなければ相対論に矛盾するわけではないと思うのだ.

これは数学か、現実の姿か

今回の計量を決めるために,時間軸とは別のもう一つの軸を使って考えたわけだが,これは思考の補助である.我々の 4 次元時空が 5 次元の中に存在していると考える必要はない.宇宙空間のどの場所も均等に曲がっていると仮定することでこの結果が出てきたのである.

考える必要はないと言われても,そういうイメージで考えたのだから,時間軸の他に 4 次元空間が存在していて,我々の世界はその中にある球の表面であり,その球は膨らんだり縮んだりしているのだと思い浮かべてしまうのが自然だろう.実際にどうなっているのかなんてまだ誰にも分からない.

今回導いた計量からどんなことが導き出せるのか,という話は別の機会にしよう.今回の話もすでに長くなったのでそろそろ休憩が必要だ.今回の計量の形のまま曲率が負になる状況というのも考えられるのだが,今回の説明で使ったイメージからは少しばかり外れてしまうのでこれも別の機会にしよう.